Nonagonal Number in Java

2025年5月9日 | 阅读 6 分钟

在本节中，我们将学习什么是九边形数，以及创建 Java 程序来检查给定数字是否为九边形数。九边形数程序经常在 Java 编码面试和学术界被问到。

九边形数

九边形数是形式为n(7n-5)/2的形数。如果 n 是九边形数，那么7n+3将是三角形数。它将三角形数和平方数概念扩展到九边形。它也称为9-边形数或enneagonal数。它是 OEIS 序列A001106。

它计算具有 9 条边的 n 个嵌套九边形图案中的点的数量。所有九边形共享一个公共顶点，其中图案中的第 i 个九边形具有由 i 个点组成的边，这些点之间的距离为一单位。N₂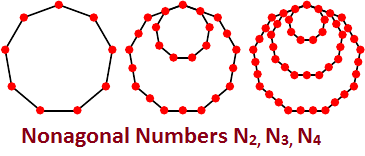

九边形数类型

中心九边形数
第二九边形数
三倍九边形数
两倍九边形数
回文九边形数

让我们详细讨论一下。

九边形数示例

前几个九边形数是

1, 9, 24, 46, 75, 111, 154, 204, 261, 325, 396, 474, 559, 651, 750, 856, 969, 1089, 1216, 1350, 1491, 1639, 1794, 1956, 2125, 2301, 2484, 2674, 2871, 3075, 3286, 3504, 3729, 3961, 4200, 4446, 4699, 4959, 5226, 5500, 5781, 6069, 6364.

求九边形数的公式

我们可以使用以下公式求第 n 个九边形数

N_n = n (7n - 5) / 2

让我们在 Java 程序中实现上述步骤。

九边形数 Java 程序

NonagonalNumberExample.java

import java.util.Scanner;
public class NonagonalNumberExample
{
//function to find nonagonal number
static int isNonagonal(int n)
{
//determines the n-th nonagonal number
return n * (7 * n - 5) / 2;
}
//driver code
public static void main(String args[])
{
Scanner sc = new Scanner(System.in);
System.out.print("Enter the term you want to find: ");
int n=sc.nextInt();
System.out.println("The "+n+" rd/th nonagonal number is: "+isNonagonal(n));
}
}

输出

Enter the term you want to find: 4
The 4 rd/th nonagonal number is: 46

中心九边形数

它也是一个形数，可以使用以下公式计算

N_n = 9n(n-1)/2+1

它是 OEIS 序列A060544。请注意，序列 A000217 中的每第三个三角形数都是九边形数。

中心九边形数示例

前几个中心九边形数是

1, 10, 28, 55, 91, 136, 190, 253, 325, 406, 496, 595, 703, 820, 946, 1081, 1225, 1378, 1540, 1711, 1891, 2080, 2278, 2485, 2701, 2926, 3160, 3403, 3655, 3916, 4186, 4465, 4753, 5050, 5356, 5671, 5995, 6328, 6670, 7021, 7381, 7750, 8128, 8515, 8911, 9316.

求中心九边形数的公式

我们可以使用以下公式计算中心九边形数

N_n = 9n(n-1)/2+1

中心九边形数 Java 程序

CenteredNonagonalNumberExample.java

import java.util.Scanner;
public class CenteredNonagonalNumberExample
{
//function to find the centered nonagonal number
static int isNonagonal(int n)
{
//determines the n-th centered nonagonal number
return 9*n*(n-1)/2+1;
}
//driver code
public static void main(String args[])
{
Scanner sc = new Scanner(System.in);
System.out.print("Enter the term you want to find: ");
int n=sc.nextInt();
System.out.println("The "+n+" rd/th centered nonagonal number is: "+isNonagonal(n));
}
}

输出

Enter the term you want to find: 25
The 25 rd/th centered nonagonal number is: 2701

第二九边形数

它也是一个形数，可以使用以下公式求得

N_n = n*(7*n+5)/2

它是 OEIS 序列A179986。

第二九边形数示例

前几个九边形数是

6, 19, 39, 66, 100, 141, 189, 244, 306, 375, 451, 534, 624, 721, 825, 936, 1054, 1179, 1311, 1450, 1596, 1749, 1909, 2076, 2250, 2431, 2619, 2814, 3016, 3225, 3441, 3664, 3894, 4131, 4375, 4626, 4884, 5149, 5421, 5700, 5986, 6279, 6579, 6886.

请注意，该序列是 OEIS 序列A118277（仅偶数部分）的二等分。

第二九边形数 Java 程序

SecondNonagonalNumberExample.java

import java.util.Scanner;
public class SecondNonagonalNumberExample
{
//function to find the second 9-gonal or nonagonal number
static int isNonagonal(int n)
{
//determines the n-th second 9-gonal number
return n*(7*n+5)/2;
}
//driver code
public static void main(String args[])
{
Scanner sc = new Scanner(System.in);
System.out.print("Enter the term you want to find: ");
int n=sc.nextInt();
System.out.println("The "+n+" rd/th second 9-gonal or nonagonal number is: "+isNonagonal(n));
}
}

输出

Enter the term you want to find: 35
The 35 rd/th second 9-gonal or nonagonal number is: 4375

三倍九边形数

还有另一个 OEIS 序列A152759，它也是一个 9-边形数或九边形数。但它是序列A001106的 3 倍。这意味着我们可以使用以下任一公式计算 3 倍 9-边形数

N_n= 3*(n*(7*n-5)/2)

或

N_n= (21n^2 - 15n)/2

或

A001106(n)*3

三倍九边形数示例

前几个三倍九边形数是

3, 27, 72, 138, 225, 333, 462, 612, 783, 975, 1188, 1422, 1677, 1953, 2250, 2568, 2907, 3267, 3648, 4050, 4473, 4917, 5382, 5868, 6375, 6903, 7452, 8022, 8613, 9225, 9858, 10512, 11187, 11883, 12600, 13338, 14097, 14877, 15678.

三倍九边形数 Java 程序

ThriceNonagonalNumberExample.java

import java.util.Scanner;
public class ThriceNonagonalNumberExample
{
//function to find 3-times nonagonal number
static int isNonagonal(int n)
{
//determines the n-th 3-times nonagonal number
return 3*(n*(7*n-5)/2);
}
//driver code
public static void main(String args[])
{
Scanner sc = new Scanner(System.in);
System.out.print("Enter the term you want to find: ");
int n=sc.nextInt();
System.out.println("The "+n+" rd/th 3-times nonagonal number is: "+isNonagonal(n));
}
}

输出

Enter the term you want to find: 10
The 10 rd/th 3-times nonagonal number is: 975

两倍九边形数

它是 OEIS 序列A139268。我们可以使用以下公式计算两倍九边形数

N_n = n(7n-5)

两倍九边形数示例

前几个两倍九边形数是

2, 18, 48, 92, 150, 222, 308, 408, 522, 650, 792, 948, 1118, 1302, 1500, 1712, 1938, 2178, 2432, 2700, 2982, 3278, 3588, 3912, 4250, 4602, 4968, 5348, 5742, 6150, 6572, 7008, 7458, 7922, 8400, 8892, 9398, 9918, 10452, 11000.

两倍九边形数 Java 程序

TwiceNonagonalNumberExample.java

import java.util.Scanner;
public class TwiceNonagonalNumberExample
{
//function to find twice nonagonal number
static int isNonagonal(int n)
{
//determines the n-th twice nonagonal number
return n*(7*n-5);
}
//driver code
public static void main(String args[])
{
Scanner sc = new Scanner(System.in);
System.out.print("Enter the term you want to find: ");
int n=sc.nextInt();
System.out.println("The "+n+" rd/th twice nonagonal number is: "+isNonagonal(n));
}
}

输出

Enter the term you want to find: 26
The 26 rd/th twice nonagonal number is: 4602

回文九边形数

回文九边形数是从两边（从右到左和从左到右）书写值不变的数字。具有偶数位数的数字不可能是回文九边形数。它是 OEIS 序列A082723。

回文九边形数示例

前几个回文九边形数是

1, 9, 111, 474, 969, 6666, 18981, 67276, 4411144, 6964696, 15444451, 57966975, 448707844, 460595064, 579696975, 931929139, 994040499, 1227667221, 9698998969, 61556965516, 664248842466, 699030030996, 99451743334715499.

回文九边形数 Java 程序

下面的 Java 程序检查给定数字是否为回文九边形数。

PalindromicNonagonalExample.java

import java.util.Scanner;
public class PalindromicNonagonalExample
{
public static void main(String[] args) 
{
int num, reversedNum = 0, remainder;
// store the number to originalNum

Scanner sc = new Scanner(System.in);
System.out.print("Enter the number you want to check: ");
num=sc.nextInt();
int originalNum = num;
//logic to reverse a number
while (num != 0) 
{
remainder = num % 10;
reversedNum = reversedNum * 10 + remainder;
num = num/10;
}
//check if reversedNum and originalNum are equal or not
if (originalNum == reversedNum) 
{
//if equal print palindromic nonagonal
System.out.println(originalNum + " is palindromic nonagonal.");
}
else 
{
//if not equal, print palindromic nonagonal    
System.out.println(originalNum + " is not palindromic nonagonal.");
}
}
}

输出 1

Enter the number you want to check: 6964696
6964696 is palindromic nonagonal.

输出 2

Enter the number you want to check: 4411144
4411144 is palindromic nonagonal.

下一个主题Java 中的异步编程

← prev next →

Nonagonal Number in Java

九边形数

九边形数类型

九边形数示例

求九边形数的公式

九边形数 Java 程序

中心九边形数

中心九边形数示例

求中心九边形数的公式

中心九边形数 Java 程序

第二九边形数

第二九边形数示例

第二九边形数 Java 程序

三倍九边形数

三倍九边形数示例

三倍九边形数 Java 程序

两倍九边形数

两倍九边形数示例

两倍九边形数 Java 程序

回文九边形数

回文九边形数示例

回文九边形数 Java 程序

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

Java Conversion

Java Misc

Nonagonal Number in Java

九边形数

九边形数类型

九边形数示例

求九边形数的公式

九边形数 Java 程序

中心九边形数

中心九边形数示例

求中心九边形数的公式

中心九边形数 Java 程序

第二九边形数

第二九边形数示例

第二九边形数 Java 程序

三倍九边形数

三倍九边形数示例

三倍九边形数 Java 程序

两倍九边形数

两倍九边形数示例

两倍九边形数 Java 程序

回文九边形数

回文九边形数示例

回文九边形数 Java 程序

相关帖子

Java 中的 AtomicIntegerArray toString() 方法及示例

Vert.x Java

Java 中函数和方法的区别

How to avoid null pointer exception in Java

Decimalstyle With positivesign() Method in Java With Examples

Java 中的排列系数

Java 中内部类的优点

Playfair Cipher Program in Java

Java 中使用字节数组反转字符串

在 Java 中获取本地 IP 地址

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器