能力倾向 高度和距离 测试 12025年3月17日 | 阅读 3 分钟 1) 两艘船在灯塔的两侧航行。从船上观察到的灯塔顶部的仰角分别为 30° 和 45°。如果灯塔高 100 米,求两艘船之间的距离。
正确选项是 (B) 答案及解释  设 AB 为灯塔的高度,C 和 D 为船的位置。 AB = 100 米,∠ACB = 45°,∠ADB = 60°  AC = AB (100 米) AC = 100 米 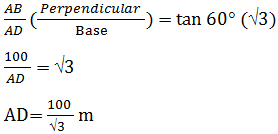 船之间的距离,CD = AC + AD  2) 一架梯子靠在墙上。它与墙壁成 60° 角。如果梯子脚和墙壁之间的距离为 5.5 米,求梯子的长度。
正确选项是 (D) 答案及解释  设 BC 为墙壁,AC 为梯子。 ∠BAC = 60° 且 AB = 5.5 米  AC = 2 * AB = 2 * 5.5 = 11 米 (选项 D) 3) 一个 1.5 米高的人离建筑物 30√3 米。当他看到建筑物顶部时,仰角为 30°。求建筑物的高度?
正确选项是 (A) 答案及解释  设 AD 为人,BE 为建筑物。 现在画一条线 DC,使 DC 垂直于 BE。 现在,BC = AD = 1.5 米 并且,DC = AB = 30√3 米  现在,建筑物的高度,BE = BC + EC = 1.5 + 30 = 31.5 米 (选项 A) 4) 在 X 点,塔顶的仰角为 30°。向塔走 30 米后,如果仰角在 Y 点变为 60°,求塔的高度?
正确选项是 (A) 答案及解释  设 AB 为塔的高度,XA 为 X 点和塔底之间的距离。  XA = 3XA - 90 - 2XA = - 90  在方程 (1) 中代入 XA 的值以求 AB(塔高)。  5) 两根电线杆的顶部由一根电线连接。电线杆的高度分别为 10 米和 14 米。如果电线与水平线成 30° 角,求电线的长度?
正确选项是 (C) 答案及解释  设 AD 和 BE 分别是高度为 10 米和 14 米的电线杆。 DE 是电线的长度 = L DC 与 AB 平行,所以 AD = BC = 10 米 所以,CE = BE - BC = 14 - 10 = 4 米  |
我们请求您订阅我们的新闻通讯以获取最新更新。