能力倾向测验：高度与距离试卷 317 Mar 2025 | 阅读 2 分钟 11) 两栋建筑物相距 40 米。 从一栋高 100 米的建筑物顶部，观察另一栋高度未知的建筑物顶部，测得俯角为 60°。 求第二栋建筑物的高度？
正确选项是 (A) 答案及解释  设第二栋建筑物 AD 的高度为 h。 EC = 100 - h DC = AB = 40  100 -h = 40 * √3 - h = -100 + 40 * 1.73 - h = -100 + 69.2 h = 30.8 米（选项 A） 12) 在 Q 点，观察一座高为 h 米的塔顶，测得仰角为 θ。 如果 Q 点与塔底之间的距离等于塔的高度，求 θ 的值？
正确选项是 (C) 答案及解释 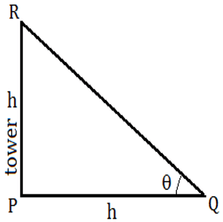 设塔 PR 的高度为 h。 PQ = h，因为 Q 点距离塔底 h 米。  tan θ=1 tanθ= 45°（选项 C） 13) 当太阳的仰角为 60° 时，一根高 3 米的杆子的阴影长度是
正确选项是 (B) 答案及解释  设阴影的长度为 AB = X 米。 塔的高度，AC = 3 米  X = √3 米（选项 B） 14) 放风筝的线长 200 米。 线完全拉直，与水平面的夹角为 60°，求风筝离地面的高度。
正确选项是 (A) 答案及解释  设风筝离地面的高度为 AC = h。 线的长度，BC = 200 米  = 100 * √l3 = 100 * 1.73 = 173 米（选项 A） 15) 一架飞机飞越两个相距 4 公里的村庄。 如果在某一时刻，从飞机上观察这两个村庄的俯角分别为 45° 和 60°，求飞机在那个时刻的高度？
正确选项是 (4) 答案及解释  设飞机在 D 点，村庄分别在 B 点和 C 点。 设飞机的高度为 AD = h。  h = X + 4 ..................(2) 将方程 (1) 中 X 的值代入方程 (2)  |
我们请求您订阅我们的新闻通讯以获取最新更新。
我们提供所有技术（如 Java 教程、Android、Java 框架）的教程和面试问题
G-13, 2nd Floor, Sec-3, Noida, UP, 201301, India
Python
Java
JavaScript
SQL
C
C++
HTML
CSS
React
Node.js
Spring Boot
C#
PHP
MySQL
MongoDB
AI
ML
DSA
DBMS
OS
Aptitude
Reasoning
