数字能力倾向概念与公式

注意事项

1) 自然数： 用于计数的计数数称为自然数，即 1,2,3,4,5,6,7,8,9。这些数字称为数码。自然数用 'N' 表示。0 称为无效数字，其他数字称为有效数字。

2) 整数： 在自然数中包含 '0' 就得到整数，即 0,1,2,3,4,5,6,7,8,9。整数是正数。它们不包含任何分数或小数部分，用 'W' 表示。

3) 整数： 包含负数但不包含分数的整数称为整数，例如 -5,-4,-3,-2,-1,0,1,2,3,4,5。因此，整数可以是正数（1,2,3,4,5）、负数（-5,-4,-3,-2,-1）或零（0）。

4) 质数： 大于 1 且只能被 1 和自身整除的整数称为质数，例如 2,3,5,7,11。

5) 互质数： 如果两个自然数 p 和 q 的最大公约数是 1，则称它们为互质数，例如 (2, 3) (4, 5) (7, 9) (11, 9)。

6) 合数： 指大于 1 且不是质数的整数。它可以被除了 1 和自身以外的数整除，例如 4,6,8,9,10,12。

7) 偶数： 能被 2 整除的整数称为偶数，例如 2,4,6,8。

8) 奇数： 不能被 2 整除的整数称为奇数，例如 1,3,5,7,9。

9) 连续数： 它们是一系列数字，其中数字按顺序一个接一个出现，即两个连续数字之间相差 1，或者每个数字都比前一个数字大 1。

10) 有理数： 形如 p/q 的数，其中 p 和 q 是整数且 q 不能为零，称为有理数，例如 22/7, 5/3, 0/11, -143/15。

11) 无理数： 用小数表示时不终止也不重复的数称为无理数。这些数不能表示为整数之比或分数，例如 √2,√3,√5, π 等。

12)实数： 可以在数轴上找到的数字，包括有理数和无理数，称为实数，例如 -1.5,√2,0,1,2,3,π。你几乎可以想象到的任何数字都是实数。

13)数字的实际值： 数字的实际值。它保持不变，不随数字的位置而改变，例如，在数字 435 和 454 中，数字 5 的实际值是 5。

14)位值： 数字的位值取决于它在数字中的位置。它是其位置和实际值的乘积。数字中的每个位置的值是其右边位置的 10 倍，例如，在数字 567 中，数字 7 在个位，数字 6 在十位，数字 5 在百位，7 的位值是 7*10⁰ = 7，6 的位值是 6*10¹ = 60，5 的位值是 5*10² = 500。

15) 个位数： 个位数是数字的个位数字。

0、1、5 和 6 的规则： 以数字 0、1、5 和 6 结尾的整数具有相同的个位数，即 0、1、5、6，分别，与正整数指数无关。

例如：156⁴ 的个位数 = 6
同样，131^1783663797 的个位数 =1

以 4 结尾的整数规则

4¹ 的个位数 = 4
4² 的个位数 = 16
4³ 的个位数 = 64
4⁴ 的个位数 = 256

这表明如果 4 的幂是偶数，则个位数是 6；如果幂是奇数，则个位数是 4。

9 的规则

9¹ = 9
9² = 81
9³ = 729
9⁴= 6561

这表明如果 9 的幂是偶数，则个位数是 1；如果幂是奇数，则个位数是 9。

2、3、7 和 8 的规则： 这些数字具有 4 个不同数字的幂周期，如下所示

2¹ =2
2² =4
2³ = 8
2⁴ = 16
2⁵ = 32
2⁶ = 64
2⁷ = 128
2⁸ = 256

它遵循一个模式：2,4,8,6, 2,4,8,6 等。

因此，2 的可能个位数有 4 个不同的数字 2、4、8 和 6。

同样

3¹ =3
3² =9
3³ = 27
3⁴ = 81
3⁵ = 243
3⁶ =729
3⁷ = 2187
3⁸ = 6561

它遵循一个模式：3, 9, 7, 1, 3, 9, 7,1 等。

因此，3 的可能个位数有 4 个不同的数字 3、9、7 和 1。

7 和 8 的逻辑相同：这些数字有 4 个可能的不同数字作为它们的可能个位数。7 分别有 7, 9, 3, 1，8 有 8, 4, 2, 6。

注意事项

1.) 数字 1 既不是质数也不是合数。

2.) 数字 2 是唯一的偶质数。

3.) 1 到 100 之间有 25 个质数，例如。

2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89 和 97。

如何判断一个给定的数字是否为质数；

• 选择最小的正整数 'n'，使得 n² > 给定的数字。
• 找出所有小于 n 的质数，并检查给定的数字是否可以被其中任何一个质数整除。
• 如果给定的数字不能被任何质数整除，那么它就是一个质数。请参阅下面的示例；

823 是质数吗？

由于 (28)² = 784 且 784<823，所以我们不考虑 28。

(29)² = 841<823，所以 n = 29

小于 29 的质数是 2, 3, 5, 7, 11, 13, 17, 19, 23

我们发现 823 不能被这些质数中的任何一个整除，所以它是一个质数。

整除性检验或整除规则

可被 2 整除： 如果一个数字的最后一位或个位数是 0 或可以被 2 整除，则该数字可以被 2 整除，例如 150, 224, 436

可被 3 整除： 如果一个数字的数字之和可以被 3 整除，则该数字可以被 3 整除，例如 246

可被 4 整除： 如果一个数字的最后两位数字可以被 4 整除，或者数字末尾有两个或多个零，则该数字可以被 4 整除，例如 516 因为 16 可以被 4 整除，而末尾有 00 的 15800 也可以被 4 整除。

可被 5 整除： 如果一个数字的最后一位是 0 或 5，则该数字可以被 5 整除，例如 500 和 505。

可被 6 整除： 如果一个数字可以被 2 和 3 整除，则该数字可以被 6 整除，例如 114

可被 8 整除： 如果一个数字的最后三位数字可以被 8 整除，则该数字可以被 8 整除，例如 1200

可被 9 整除： 如果一个数字的数字之和可以被 9 整除，则该数字可以被 9 整除，例如 117

可被 10 整除： 如果一个数字的最后一位是 0，则该数字可以被 10 整除，例如 230

可被 12 整除： 如果一个数字可以被 3 和 4 整除，则该数字可以被 12 整除，例如 264

可被 25 整除： 如果一个数字的最后两位是零，或者其最后两位数字组成的数可以被 25 整除，则该数字可以被 25 整除，例如 300 和 325。

一些重要公式

i. (a+b)² = a² + b² + 2ab

ii. (a - b)² = a² + b² - 2ab

iii. (a+b)² - (a - b)² = 4ab

iv. (a+b)² + (a - b)² = 2 (a² + b² )

v. (a² -b²) = (a - b) (a+b)

vi. (a³+b³) = (a+b) (a² - ab + b²)

vii. a³- b³ = (a - b) (a² + ab + b²)

viii. a.( b + c) = ab + ac

ix. a.( b - c) = ab - ac

x. (a+b)³ = a³ + b³ + 3ab (a+b)

xi. (a - b)³ = a³ - b³ - 3ab (a - b)

快速乘法方法

1.) 将一个数乘以 9, 99, 999, 9999 或 10ⁿ - 1：在被乘数的右边加上与乘数中的九位数一样多的零，然后从结果中减去被乘数。请参阅下面的示例；

a.) 2789 * 99 = ?

2789 (被乘数) x 99 (乘数) = 278900-2789= 276111

b.) 234 * 999 = 234000 - 234 = 233766

2. 将一个数乘以 11, 101, 1001, 10001 或 10ⁿ +1：在被乘数的右边放置 'n' 个零，然后将被乘数加到它上面得到答案。请参阅下面的示例；

a.) 234 * 11 (10¹ + 1)= 2340 + 234 = 2574

b.) 234 * 101 (10² + 1)= 23400 + 234 = 23634

3.) 将一个数乘以 5, 25, 125, 625 或乘以 5 的某个幂的数：在被乘数的右边放置与乘数中 5 的幂次方相等的零数，然后将其除以 2 的 5 次幂。请参阅下面的示例；

一些更快的 H方法

o 当一个数除以 d₁ 和 d₂ 时分别留下余数 r₁ 和 r₂。如果该数除以 d₁ * d₂，则余数由下式给出；

= (d₁* r₂+r₁)

o 当两个数除以给定的除数时分别留下余数 r₁ 和 r₂。如果这两个数的和除以相同的除数得到的余数是 r₃。那么除数由下式给出；

= r₁ + r₂ - r₃

o 如果给出了两个数字（x 和 y）的和与差，那么它们的乘积由下式给出；

o 并且，这两个数字由下式给出；

如何找到可被给定整数整除的数字的数量

让我们通过一个例子来理解；找出 432 以下可以被 15 整除的数字的数量。

方法： 将 432 除以 15。

432 = 28 (商) * 15 + 12

得到的商是 432 以下可被 15 整除的数字所需的数量。

计数数字的基本规则

o 前 n 个自然数的和由下式给出；

o 前 n 个奇数的和由下式给出；

和 = n²

o 前 n 个偶数的和由下式给出；

和 = n (n+1)

o 前 n 个自然数的平方和由下式给出；

o 前 n 个自然数的立方和由下式给出；

数列： 指以逻辑模式前进的数字序列，例如等差数列和等比数列等。

等差数列： 指数字序列中任意两个连续数字之间的差保持不变，例如数列 1,2,3,4.., 3,5,7,9.. 和 5,10,15,20...

等差数列的第一项用 'a' 表示，第 n 项用 T_n 表示，公差用 'd' 表示，前 n 个数字的和用 'S_n' 表示，例如，在等差序列 1,2,3,4,5 中，a = 1, d = 2-1=1，T₃ = 3。

因此，首项为 'a'，公差为 d 的等差数列由下式给出；

a, (a+d), (a+2d), (a+3d),

o 等差数列的第 n 项由下式给出；

T_n = a + (n-1)d

o 等差数列前 n 项的和由下式给出；

o 等差数列中的项数由下式给出；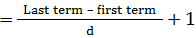

等比数列： 指数字序列，其中每个数字是通过将前一个数字乘以一个固定数或公比得到的。

等比数列的第一项用 'a' 表示，第 n 项用 T_n 表示，公比用 'r' 表示，前 n 个数字的和用 'Sⁿ' 表示，例如，在等比数列 3,9,27,81 中，a = 3, r = 9/3 或 3，T₃ = 27。

因此，首项为 'a'，公比为 'r' 的等比数列由下式给出；

a, ar, ar²,ar³,-

o 等比数列的第 n 项由下式给出；

= ar^n-1

o 等比数列前 n 项的和由下式给出；

数字能力倾向测试题