加法定义

加法（通常用加号 (+) 表示）是四种基本数学运算之一，包括减法、乘法和除法。当两个整数相加时，结果就是这些值的总和或总数。

除了计数项目外，加法还可以通过使用抽象的数字（包括整数、实数和复数）来定义和执行，而无需参考具体的对象。算术是数学的一个分支，将包括加法。加法还可以在代数中对抽象对象（如向量、矩阵、子空间和子群）进行运算，代数是数学的另一个分支。加法是我们日常生活中最重要的数学函数之一。我们在各种情况下都会用到数字相加。加法最典型的日常应用之一是在处理时间或金钱时，例如计算发票和收据。加法有几个重要的性质。它具有交换性，这意味着操作数的顺序无关紧要；它具有结合性，这意味着当两个以上的整数相加时，执行加法的顺序无关紧要。计数与重复加1相同。加0不会改变数字。

加法遵循可预测的规则，例如相关的运算（如减法和乘法）。加法是最基本的数字运算之一。儿童可以相加非常小的数字，因为像“1+1”这样最基本的任务可以由小到五个月的婴儿以及其他一些动物物种的成员完成。小学教育的学生学习以十进制系统相加数字，从个位数开始，然后逐渐解决更困难的问题。机械辅助工具从古老的算盘扩展到现代计算机，关于最有效的加法实现的研究仍在进行中。算术的四种基本运算之一是将一个或多个整数相加以获得一个新值。对于大数字，加法通常更方便地将它们写成一列并在底部计算。在这种情况下，总和是数字列表的加法，其符号表示为∑。

加法的性质

两个或多个数字的加法具有各种重要的性质。以下加法性质列表将有助于预测在加法过程中获得的结果的符号

• 两个整数的和也是一个整数。
• 两个自然数的和仍然是自然数。
• 两个整数的和是一个整数。相反，两个正整数的和是正整数，两个负整数的和是负数，一个正整数和一个负整数的和是与最大数符号相同的整数。
• 两个有理数的和将得到一个有理数。此外，与正负号相关的性质将与整数相同。
• 任何数乘以0结果都是其本身。

加法方法

数学中加法有几种方法，包括

• 计数（用手指）
• 使用数轴
• 重组
• 使用加法表

加法的组成部分

加法语句可以分解为以下组成部分。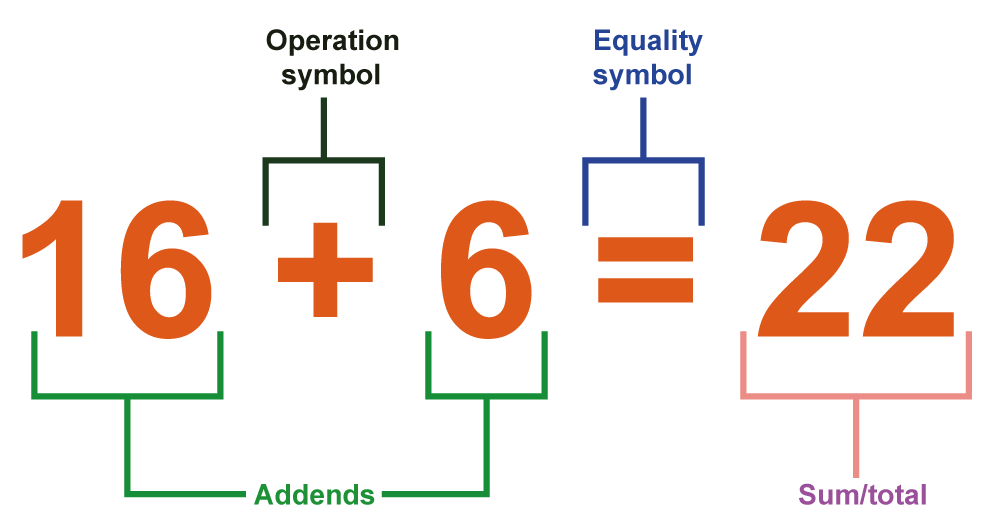

• 加数
  被加的数字称为加数。进行加法运算时，您将加数合并以产生一个和。
• 加号
  加数之间有一个加号 (+)。如果句子是水平书写的，则在和之前放置一个“等于”符号 (=)。
• 求和
  和是加数相加后获得的最终结果。它表示加数的组合值或总值。

如何计算加法总和？

在解决加法和时，可以相加一位数，但对于更大的数字，我们根据它们的位值（如个位、十位、百位、千位等）将它们分成列。

根据位值系统，我们总是从右侧开始加法。这意味着我们从个位开始，然后是十位，然后是百位，依此类推。在处理这种情况时，我们可能会遇到有进位和无进位的情况。在接下来的部分中，我们将探讨带重组的加法和不带重组的加法。

不带重组的加法

不带重组的加法是指每列数字之和小于或等于9的情况。让我们通过一个例子来学习如何在不带重组的情况下相加两个或更多数字。

例如，将11234加到21123。我们将采取以下步骤并将其与下图关联。

• 步骤1： 从个位的数字开始。(4 + 3 = 7)
• 步骤2： 转到十位的数字。(3 + 2 = 5)
• 步骤3： 现在，将百位的数字相加。(2 + 1 = 3)
• 步骤4： 将千位的数字相加。(1 + 1 = 2)
• 步骤5： 最后，将万位的数字相加。(1 + 2 = 3)
• 步骤 6 11234 + 21123 = 32357

此外，我们将每个位值列中的数字相加，然后不重新分组地得到结果。现在让我们看看带重新分组的加法。

带重组的加法

在进行加法运算时，如果任何一列中的加数之和大于 9，我们就会将这个数量重组为十位和个位。和的十位数字会进位到前一列，而和的个位数字则写在那一列中。换句话说，我们将个位数字写在那一列中，同时将十位数字移到紧邻的左侧一列。通过一个例子，让我们学习如何使用重组来添加两个或更多数字。

例如，将3475加上2865。

请遵循以下说明并尝试理解它们。

• 步骤 1： 从个位的数字开始。（5 + 5 = 10）。在这种情况下，总和是 10。和的十位数字 1 将进位到前一列。
• 步骤 2： 将十位数字与进位 1 相加。这意味着 1（进位）+ 7 + 6 = 14。在这种情况下，总和是 14。和的十位数字 1 将进位到百位。
• 步骤 3： 现在将百位数字与进位数字 1 相乘。这意味着 1（进位）+ 4 + 8 = 13。在这种情况下，总和是 13。和的十位数字 1 将进位到千位。
• 步骤 4： 将千位数字与进位数字 1 相乘，得到 1（进位）+ 3 + 2 = 6。
• 步骤 5： 因此，3475 + 2865 等于 6340。

注意

加法的一个基本性质是改变数字的顺序不会改变结果。例如，颠倒加数会得到相同的值 (2865 + 3475 = 6340)。这被称为加法交换律。

数轴加法

另一种加数的方法是使用数轴。让我们通过一个例子来看看数轴上的加法。

使用数轴，计算 10 + 3。

首先，在数轴上标记数字 10。当我们在数轴上添加一个数字时，我们通过一次向右滑动一个数字来计数。我们将向右移动三步，将 10 和 3 相加。这使我们到达数字 13。因此，10 + 3 等于 13。

加法术语

在一般加法中，要相加的数字或对象统称为项、加数或和数，同样的术语也适用于多个项的求和。这与相乘的因子不同。有些作者将第一个加数称为被加数。许多文艺复兴时期的作者根本不认为第一个加数是“加数”。由于加法的交换性，今天很少使用“被加数”这个名称，并且两个术语通常都称为加数。上面使用的所有词汇都源自拉丁语。

“加法”（Addition）和“加”（add）这两个英文词源自拉丁动词 addere，它是 ad “to”和 dare “to give”的复合词，两者都源自原始印欧语根 *deh3- “to give”，所以“加”就是“给予”。使用动名词后缀 -nd 得到“addend”，意思是“要加的东西”。类似地，从 augere “增加”得到“augend”，“要增加的东西”。“Sum”和“summand”源自拉丁名词 summa，意思是“最高的，顶部的”，以及相关的动词 summare。这不仅相关，因为两个正数的和大于其中任何一个，还因为古希腊和罗马人通常向上加，而不是现代的向下加，所以和高于加数。Addere 和 summare 可以追溯到波伊提乌，如果不是更早的罗马作家，如维特鲁威和弗龙提努斯。波伊提乌还使用了几个不同的名称来表示加法运算。乔叟推广了后来的中古英语术语“added”和“adding”。加号“+”是拉丁词 et 的缩写，意思是“和”。它最早出现在 1489 年的数学著作中。

加法中的解释

许多物理过程都使用加法进行建模。即使对于自然数相加的简单情况，也有多种解释和图形表示。

• 组合集合
  集合的组合可能是对加法最基本的理解，它可以定义为：当两个或多个不相交的集合合并为一个单一的集合时，单一集合中的对象数量等于原始集合中对象数量的总和。这种解释很简单，歧义的风险很小。它在高等数学中也很有用。然而，尚不清楚如何将这种形式的加法扩展到包括分数或负数。一种可能的方法是检查易于分割的对象的集合，例如馅饼，或者更好的是分段的杆。杆可以首尾相连，而不是简单地连接段的集合，这说明了加法的另一个原理：添加杆的长度而不是杆本身。
• 延长长度
  将初始长度延长一定长度是加法的第二个含义，可以定义为，当初始长度延长特定数量时，其最终长度是原始长度和延长长度的总和。在代数意义上，和 a + b 可以理解为结合 a 和 b 的二元运算，或者可以解释为将 b 加上更多单位到 a。在后一种解释中，和 a + b 的部分具有不对称的作用，并且运算 a + b 被理解为将一元运算 +b 应用于 a。因为 a 扮演着被动角色，所以将其称为被加数比将 a 和 b 都称为加数更合适。因为每个一元加法运算都有一个逆一元减法运算，并且一元方法也有助于解决减法。

加法性质

交换律

加法具有交换性，这意味着改变和中项的顺序会产生相同的结果。如果 a 和 b 代表任意两个数字，那么

“加法交换律”或“加法交换性质”指的是加法是可交换的。一些二元运算（如乘法）是可交换的，但许多其他运算（如减法和除法）则不是。

结合律

加法是结合的，这意味着当三个或更多数字相加时，运算顺序不影响结果。例如，表达式 a + b + c 应该定义为 (a + b) + c 还是 a + (b + c)？鉴于加法是结合的，所选择的定义是无关紧要的。对于任意三个数字 a、b 和 c，(a + b) + c = a + (b + c) 都是正确的。例如，(1 + 2) + 3 = 3 + 3 = 6 = 1 + 5 = 1 + (2 + 3)。

当加法与其他运算结合使用时，运算顺序至关重要。在传统的运算顺序中，加法排在幂运算、n次根、乘法和除法之后，但与减法同级。

恒等性质

将零加到任何数字都不会产生任何影响，因此零是加法的单位元，通常称为加法恒等元。在符号中，可以表示为 a + 0 = a。

这项定律首次在婆罗摩笈多的《婆罗摩历算书》中于公元628年被提出，尽管他将其写成三个独立的定律，取决于 an 是负数、正数还是零本身，并且他使用文字而非代数符号。后来的印度数学家发展了这一概念。例如，在公元830年，摩诃毗罗说：“零加上什么就变成什么”，这对应于一元断言 0 + a = a。巴斯卡拉在12世纪评论道：“在零的加减法中，数量，无论是正数还是负数，都保持不变”，这对应于一元断言 a + 0 = a。

后继数

在整数的语境中，加一具有特殊的含义：对于任意整数 a，整数 (a + 1) 是最小且大于 a 的整数，通常称为 a 的后继数。3 是 2 的后继数，7 是 6 的后继数。由于这种后继关系，a + b 的值也可以看作 a 的后继数，从而导致迭代后继的加法。6 + 2 等于 8，因为 8 是 7 的后继数，而 7 是 6 的后继数，使得 8 是 6 的第 2 个后继数。

加法的单位

为了对物理值进行数值加法，它们必须以标准单位表示。将 50 毫升加到 150 毫升会得到 200 毫升。然而，如果将 5 英尺的测量值延长 2 英寸，总长度是 62 英寸，因为 60 英寸与 5 英尺是同义的。但是，尝试将 3 米和 4 平方米相加通常是没有意义的，因为这些单位是不可比的，这种考虑在量纲分析中是基本的。

加法技巧

• 诸如“放在一起”、“总共”、“全部”和“总计”之类的词语表示您必须将指定的数字相加。
• 从较大的数字开始，然后乘以较小的数字。例如，将 12 加到 43 比将 43 加到 12 更容易。
• 为了使加法更容易，将整数按位值划分。例如，22 + 64 可以分解为 20 + 2 + 60 + 4。虽然这很有挑战性，但它使心算变得容易。
• 当添加多位数字时，将它们按位值对应的列依次排列。
• 当将零加到任何整数时，您会得到该整数本身。
• 当 1 加到任何数字时，结果是该数字的后继数。
• “+”号用于表示加法。
• 您添加一系列数字的顺序无关紧要，总和保持不变。例如，2 + 5 + 3 等于 10，而 5 + 3 + 2 等于 10。这被称为加法的结合律。

结论

加法是一种基本的数学运算，通过组合两个或多个数值。这个过程在我们的日常生活中使用，简单的例子包括计算金钱、计算时间、计算班级中的学生人数等。这个运算用“+”（加号）表示。它通常用于日常任务，如计数、测量和计算。加法是一个简单而基本的概念，它是更复杂数学运算的基础，并且对于解决各种领域和专业的数学问题至关重要。此外，加法在数学和各种现实世界环境中都很有用，例如计算预算、测量数量和解决日常困难。