周角定义

当两条射线在一个点（称为顶点）相遇时，就形成了一个称为角的几何形状。角的度量由两条射线之间的旋转度数决定，通常以度、弧度或梯度表示。角在几何学中至关重要，用于定义两条线或平面之间的连接，并量化形状和物体的大小。通过这种方式，角是理解和检查几何图形特征的有用工具。

角度类型

根据度量方式和位置，几何学中有许多不同类型的角。以下是一些最常见的角：

锐角

锐角小于 90 度。

直角

直角正好是 90 度。在示意图中，它通常用一个小方块表示。

钝角

大于 90 度但小于 180 度的角被认为是钝角。

平角

平角是 180 度。一条直线将平面分成两半。

优角

大于 180 度但小于 360 度的角称为优角。

余角

余角的总和正好是 90 度。

补角

互补角是指它们的和正好是 180 度的角。

对顶角

两条直线相交形成的两个不相邻的角称为对顶角。它们的度数总是相同，并且是全等的。

理解各种类型的角至关重要，因为它们的独特品质和关系可用于解决问题和分析几何对象。

周角定义

测量正好为 360 度的角被称为周角。它由两条向相反方向延伸的射线组成，它们完全围绕着它们的共同顶点。换句话说，绕一个点完整旋转一圈构成一个周角。在示意图中，它通常用一个小圆圈表示。

周角具有几个重要的特征。首先，任何 360 度倍数的角（例如，720 度、1080 度等）都是周角。此外，任何两个角之和为 360 度的角都是互补的，这使得它们可以结合起来形成一个周角。最后，周角是衡量其他角的标准。例如，半旋转（180 度）通常用作衡量其他角的标准，因为它代表整个旋转的一半。

周角在物理学、工程学和数学等多个学科中至关重要。它们用于分析旋转物体和系统的运动，并定义圆形、球体和其他弯曲物体的特征。

周角示例

周角的示例

• 时钟的时针每 12 小时完成一次完整旋转，即 360 度，相当于一个周角。
• 地球每 24 小时绕其轴线旋转 360 度，完成一次完整旋转。
• 当汽车或自行车轮行驶相当于其周长（即车轮半径的两倍）时，它已完成一次完整旋转。这与 360 度旋转相同。
  
• 行星绕太阳的完整旋转：太阳系中行星绕太阳完整旋转一次所需的时间因行星而异。例如，地球在 365.24 天内旋转 360 度，即一次完整革命。
• 体操或舞蹈中的完整转体通常需要绕垂直轴完整旋转 360 度。

这些只是使用周角的几个例子。通常，360 度的周角可以表示涉及绕给定点或轴的完整旋转或公转的任何情况。

周角特征

周角具有几个重要的特性，包括：

• 一个周角是 360 度。
• 任何 360 度倍数的角都是周角。
• 任何总和为 360 度的互补角都可以组合起来形成一个周角。
• 周角是多边形中所有其他角的总和。例如，三角形的总角是 180 度，或周角的一半。
• 通过减去或加上 360 度的倍数，每个大于 360 度的角都可以转换为 0 到 360 度之间的等效角。
• 可以使用周角作为标准来测量附加角。例如，半旋转（180 度）通常用作衡量其他角的标准，因为它代表整个旋转的一半。
• 任何 360 度倍数的角的正弦、余弦和正切值与 0 到 360 度之间相应的角的值相同。这是因为这些三角函数是周期性的。

理解周角的性质对于分析和解决涉及多边形、圆形和其他几何形状的问题至关重要。三角学是一门研究三角形的角和边之间关系的数学领域，周角及其特征在其中占据重要地位。

周角的应用

周角有几个实际用途，包括：

导航

为了确定行驶方向并计算地点之间的距离，周角用于导航，尤其是在航空和海运业。球面坐标也用于导航，它需要确定三维中的角。

天文学

在天文学中，周角解释了天体彼此之间以及与观察者的位置。天文学家在测量天空中的角度时，使用基于天赤道和天极的坐标系。

工程

为了构建和分析齿轮、涡轮机和电机等旋转结构，周角被用于工程学。工程师使用微积分和三角学来确定旋转物体运动中涉及的力和扭矩。

摄影和摄像

周角在这两种媒介中都用于管理照片和视频的排列和构图。例如，使用周角和鱼眼镜头捕捉广阔的视野或倾斜的视角可以产生戏剧性的效果。

体育

涉及旋转运动的运动，例如体操、跳水和花样滑冰，使用周角。运动员应用物理学和生物力学定律来执行复杂的动作并提高他们的表现。

游戏

视频游戏使用周角来管理虚拟角色和物体的移动和旋转。视频游戏制作者使用数学模型和算法来复制逼真的物理和运动。

这些只是周角在实际情况中使用的几个例子。通常，角度及其特征可用于解释涉及旋转、方向或位置的任何场景。

如何测量周角

您必须围绕给定点或轴完成一次完整旋转才能测量周角。您可以通过物理旋转物体或身体、使用量角器或其他测量设备，或两者兼而有之来完成此操作。

如果您使用量角器，请将基线沿角度的一侧放置，并将量角器的中心放在角度的顶点处。当角度的另一侧与量角器上的刻度相交时，请读取该处的测量值。如果角度是周角，则测量值为 360 度。

如果您物理旋转物体或您的身体，请标记起点并围绕固定点或轴完成一次完整旋转。然后，使用量角器或其他测量设备，确定起始位置和结束点之间的角度。同样，如果角度是周角，则测量值为 360 度。

周角是一个特例，在现实世界中并不常见；记住这一点至关重要。可以测量锐角、钝角和直角，它们构成了我们遇到的大多数角度，使用与周角相同的方法。

旋转与周角的关系

由于这两个概念都涉及围绕固定点或轴的完整旋转，因此周角和旋转直接相关。

一个完整旋转等于一个周角，其长度为 360 度。换句话说，完整旋转衡量物体或系统完成完整旋转的次数，而周角衡量物体或系统围绕固定点或轴旋转的量。

这种关系经常用于物理学、工程学和其他旋转运动学科。例如，当确定物体的角速度时，每单位时间的旋转次数通常用于衡量物体的旋转速率。

同样重要的是要注意，圆周运动是物理学中的一个关键概念，与周角和旋转的概念密切相关。当物体围绕固定点或轴沿圆形路径移动时，沿路径行驶的距离与物体旋转的角度成正比。

在微积分和三角学中使用周角

周角用于微积分中研究周期函数，这些函数的值随时间重复出现。周期函数可以模拟各种物理事件，包括波和振荡。为了求解方程和进行预测，周期函数分析检查它们的特征，例如振幅、周期和相位偏移。

总而言之，对周角在三角学和微积分中的使用，以及这些思想在物理学、工程学和其他学科中对现实世界问题的应用，取决于对循环函数和周期现象行为的理解。

周角在 3D 几何中的作用

周角在三维几何和球面坐标中的作用。

球面坐标是用于描述三维空间中点的坐标系，3D 几何学严重依赖周角。

从原点的距离 (r)、正 z 轴与半径向量之间的角度 () 以及正 x 轴与半径向量在 xy 平面上的投影之间的角度 () 是用于定义球面坐标中点的三个值。

角度测量 z 轴的完整旋转。因此它是一个周角。结果，任何两个相差 2 倍的值代表空间中的相同位置，并且这些值以 2 为周期。

在研究球对称性时，周角在球面坐标中起着至关重要的作用，球对称性是围绕轴或固定点对称物体的质量。球面坐标经常用于解释许多物理系统（包括行星、恒星和分子）的特性和行为。

周角也用于 3D 几何中描述物体在三维中的旋转方式。旋转角度，其范围从 0 到 360 度（或 0 到 2 弧度），并以度或弧度测量，表示三维物体围绕固定轴的旋转。360 度（或 2 弧度）的角度表示轴的完整旋转。

关于周角的常见误解和错误

周角是常见的误解和错误的根源，这可能导致科学和数学中的混淆和错误。以下是一些最典型的误解：

• 一种典型的误解是将周角与其他角度混淆，例如优角或平角。虽然这些角度和周角相关，但它们并不相同。
• 另一个典型的错误是像测量其他单位（例如分或秒）一样考虑周角，而不是记住它们是以度或弧度测量的。
• 周角的周期为 360 度（或 2 弧度），这意味着任何两个相差 360 度（或 2 弧度）倍数的角度表示相同的角度。这是对周角周期性的错误解释。重要的是要记住，这种周期性仅适用于周角，而不适用于其他角度。
• “旋转”和“革命”这两个词可以互换使用，尽管它们都涉及物体围绕固定点或轴的运动，但革命和旋转是不同的概念。革命是指围绕固定点或轴的完整转动，而旋转可以指任何旋转角度，不一定是周角。

周角在历史和文化中的重要性

周角的历史和文化意义可以通过多种方式体现：

古代天文学和占星术

许多古代文明，包括埃及人、巴比伦人和希腊人，对天体的运动有了透彻的了解。他们使用周角来理解和预测天文事件，例如太阳、月亮和星星的运动。这些信息构成了早期占星术和天文学的基础。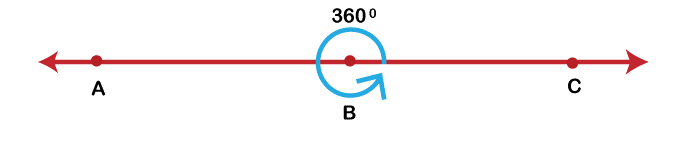

日历和计时

周角的概念与时间划分为天、小时和分钟密切相关。古代文明使用天文观测（例如太阳和星星的运动）创建日历。太阳的周期性过程被分成 365 或 360 段，使用 360 度的周角，这构成了日历和计时系统的基础。

探索和导航

周角在历史上对两者都至关重要。探险家和航海家利用天文观测（例如太阳、月亮和星星的位置）来确定他们的位置并规划他们的旅程。理解周角有助于他们理解地球的自转及其对天体的影响。

文化象征主义

周角和完整旋转在许多不同的文明中具有象征意义。周角与完整性、完成和循环相关。它经常作为和谐、团结和无限潜力的隐喻。周角可以在艺术品、宗教符号和文化仪式中象征精神或宇宙特征。

数学和科学的发展

周角的概念对数学和科学的发展至关重要。几何学、微积分和三角学都主要依赖于理解和计算周角。它们为理解波现象、圆周运动以及许多其他科学和数学概念奠定了基础。如果我们了解周角的历史和文化意义，我们就能更好地理解周角在影响人类知识、探索和理解宇宙方面的作用。