数学中的整数定义

整数 (Integer) 这个词源于拉丁语，意为完整的。整数之所以被认为是独特的集合，是因为它们包含负数、正数和零，而不包含分数和小数。

整数的常见例子有 -1, -2, -3, -4, -5, 5, 3, 2, 1 ...

整数的类型

整数有三种类型：负数、正数和零。整数的全面分类包括自然数、偶数、奇数、质数、整数、合数等。

在数轴上表示整数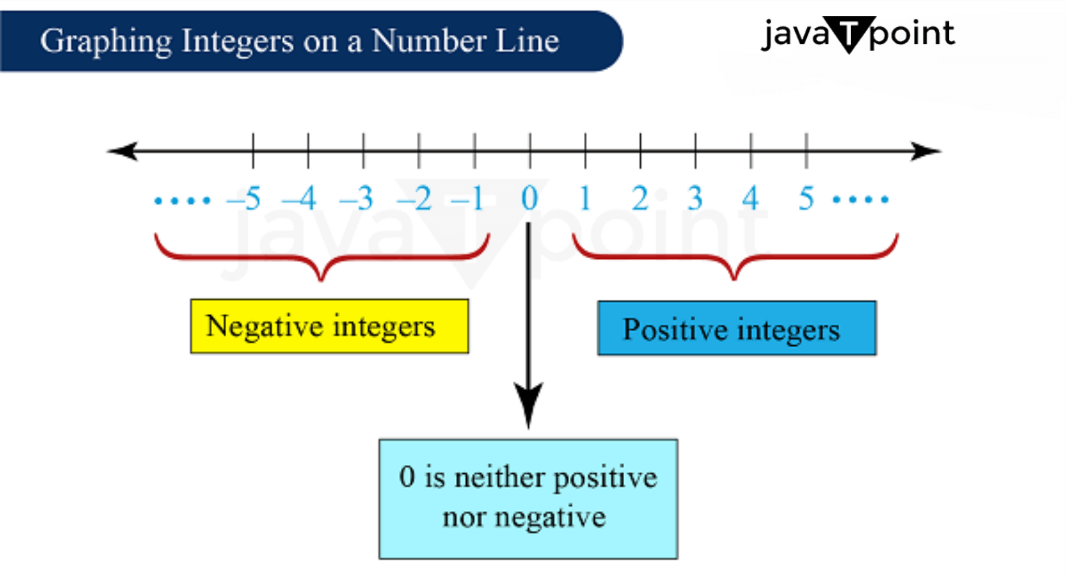

数轴是数字的图形表示。正数表示在数轴的右侧，负数表示在数轴的左侧。零位于数字的中心。

整数的历史

整数的概念出现在 1563 年。Arbermouth Holst 沉迷于他的兔子实验。他连续六个月数笼子里的兔子，发现兔子数量增加了。由此，他萌生了一个想法，开发一个用于加法和乘法的数字系统。他花了近 15 年才提出了数字系统的概念。

后来，这项工作由日本数学家在 19 世纪 90 年代继续进行，他们提出了称为整数的概念。拉丁语的意思是“未触及”。印度人、巴比伦人和玛雅人独立发明了零。一些研究人员指出，巴比伦人的发现影响了印度的数字系统。

印度数学家支持了零的概念，在此之前，零的正式创建未得到任何国家的认可，直到它传播到印度次大陆。负数在 19 世纪才被数字系统接受。

• 印度贡献

印度数学家 Brahmagupta 在公元 630 年左右因使用负数而闻名。此时，正数用于表示资产，负数用于表示负债（债务）。

• 中国贡献

中国人因使用负数而闻名，他们是第一个认识到并使用负数的文化。负数使用红色的竹竿表示。

• 欧洲贡献

欧洲人从 1545 年开始使用负数，意大利数学家Girolamo Cardano 提出负数会非常有用。

代数在阿拉伯世界的进一步发展加深了对整数的理解。法国数学家费马为现代数论奠定了基础。

当代人对整数的概念是整数的高级阶段，它们被用于金融、物理、计算机编程、工程和物理等不同领域。对整数的研究和持续研究仍然活跃。

整数加法规则

整数减法规则

整数乘法规则

整数除法规则

整数的性质

1. 加法单位元律

任何整数与零相加，值都不改变。

例如

9 + 0 = 9

2. 乘法单位元律

任何整数与 1 相乘，值都不改变。

例如：

-9 x 1 = -9

3. 加法逆元律

整数与其加法逆元相加等于零。

例如

-5 + 5 = 0

4. 整数的零乘法性质

任何数与零相乘都得到零。

例如

-10000 x 0 = 0

问题：求以下表达式的值

1. 22 - ( -45)
2. 45 + (-10)
3. - 56 + -40
4. -34 - (-60)

解决方案

1. 22 - (-45) = 22 + 45 = 67
2. 45 + (-10) = 45 -10 = 35
3. -56 + - 40 = -96
4. -34 - (-60) = -34 + 60 = 26