对顶角定义

在几何学中，当两条线相交时，会形成角。在两条线的交点处会形成四个角。对顶角是两条线相交时直接相对的角。对顶角之所以如此命名，是因为它们具有相同的顶点，但位于相交线的不同侧面。

对顶角与其他角有一些显著的特征。其中一个最重要的特征是，对顶角是全等的。全等描述的是大小或度量相同的角。 因此，一旦你知道一个对顶角的度量，你也就知道了另一个对顶角的度量。利用这个属性可以解决对顶角问题。

对顶角总是相等的另一个特征。这意味着无论相交线如何放置，对顶角都将始终相等。任何对顶角，无论是锐角（小于90度）、直角（恰好90度）还是钝角（大于90度），都具有此属性。此特征有助于证明几何定理和解决与角度相关的问题。

在数学和科学的许多分支中，对顶角都很重要。它们在几何学中用于解决需要角度和证明定理的问题。它们还用于三角学，即研究三角形的角和边如何相互关联的学科。对顶角在工程学中用于建造结构和建筑物，并在物理学中用于研究光学和光。

总之，对顶角是几何学中的一个重要课题。它们彼此相对，由两条线的交点形成。全等性和相等性是对顶角的两个关键特征，这使它们有助于解决与角度相关的问题。希望在几何学和相关领域取得成功的学生必须理解对顶角。

对顶角的性质

当两条线相交时，会形成一种叫做对顶角的角。由于一些特征，这些角与其他角不同。对顶角的全等性是它们最重要的特征之一。

对顶角总是全等的，因为它们具有相同的度数。因此，如果角A和角B是对顶角，它们的度数将相等。此特征有助于证明几何定理和解决与角度相关的问题。

对顶角的相等性是另一个重要特征。在这种情况下，“相等性”指的是角的度数。对顶角总是相等的，与某些其他角不同，包括补角或余角。这意味着如果你知道一个角的大小，你也知道另一个角的大小。相等性属性有许多用途，例如建筑结构和建筑物。

对顶角与其他类型角的线性关系是它们的另一个特征。例如，相邻角是当两条线重叠并形成一对对顶角时形成的另一对角。这些相邻角组合在一起形成一个180度的平角。线性对定理是这种关系的结果，可以应用于涉及角度的问题。

对顶角的对称性是一个关键特征。通过两个对顶角的顶点画一条线可以形成两对全等的角。这是因为对顶角在相交线的两侧对称放置。这种对称特征的应用包括光学和光的研究等。

由于一些重要特征，对顶角是独特的，有助于解决涉及角度的问题。虽然它们的线性和对称性质在工程、物理和光学等领域有许多应用，但它们的全等性和相等性在证明几何定理和解决问题方面特别有用。任何学习几何或相关学科的人都必须理解对顶角的特征。

对顶角的例子

对顶角是一个常见的几何概念，可以在许多现实世界中找到。这些角是在两条线相交时形成的，它们彼此相对。以下是一些在日常生活中可以找到对顶角的例子

建筑中结构的创建和建造经常使用对顶角。例如，屋顶与地面成一定角度建造时，会形成两对对顶角。理解对顶角的特性对于建筑设计和施工至关重要。

在导航中，物体的T点使用对顶角计算。例如，如果你正在航海，发现一座灯塔，你可以使用对顶角计算灯塔的高度。通过利用这些知识，可以安全地导航船舶。

在测量中，通过使用对顶角测量物体的高度，这也有助于制作精确的地图。测量员使用专用设备计算对顶角，这有助于制作精确的地图和图纸。

对于物理学中的光学和光的研究，对顶角至关重要。棱镜在光线穿过时扭曲并将其分离成多种颜色。由于不同的入射角和折射角导致两个对顶角，因此会发生色散。

在工程学中，对顶角用于桥梁和其他结构的设计。例如，在河流上建造桥梁时，可以使用桥梁顶部的对顶角计算水面以上的高度。为了确保桥梁牢固安全，这些信息至关重要。

总而言之，对顶角可以在各种现实世界的应用中看到，包括测量、导航和建筑设计。许多学科，包括物理学和工程学，都需要理解对顶角的特性。对顶角有许多用途，通过理解这些用途，我们可以更好地理解对顶角对我们的日常生活和我们所处的环境的重要性。

对顶角定理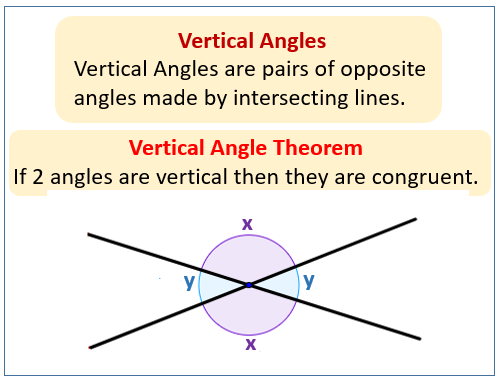

根据这个定理，当两条线相交时形成的对顶角总是全等的。换句话说，一个对顶角的大小与另一个对顶角的大小相同。

基本几何概念可用于证明对顶角定理。你可以画两条相交线并识别形成的角来证明该定理。然后可以使用角加法公设来证明两对对顶角是全等的。

例如，假设我们有两条相交线AB和CD，并且角ACD和BDC是对顶角。我们可以使用以下步骤证明这些角是全等的

• 画一条穿过点A和C的直线。
• 标记由线AB、CD和AC的交点形成的角。
• 使用角加法公设写出角ACD的度量方程。例如，我们可以写：m?ACD = m?ACB + m?BCD。
• 对角BDC重复步骤3。我们可以写：m?BDC = m?BDA + m?ADC。

请注意，角ACB和BDA是内错角，角ADC和BCD是内错角。根据内错角定理，这些角是全等的。因此，我们可以将它们的度量代入我们在步骤3和4中写的方程。

• 简化方程以显示m?ACD = m?BDC。这证明了两个对顶角是全等的。

对顶角定理在几何学和相关学科中有许多关键应用。例如，它用于证明对应角定理和内错角定理这两个几何性质。此外，它还用于几何模型的创建和代数证明。

对顶角定理是对顶角的一个关键特征，总而言之。它断言由两条线相交形成的对顶角总是全等的。该定理在几何学和相关领域中有许多重要应用，并且可以使用基本几何概念进行证明。

对顶角的应用

对顶角在广泛的数学和科学领域中广泛使用。以下是对顶角的一些主要用途

• 几何学是对顶角有重要应用的领域之一。许多几何定理都可以用它们来证明。例如，对顶角定理可以用来阐述对应角定理，该定理指出，如果两条平行线被一条截线相交，那么对应角是全等的。这个定理是许多其他概念的基本组成部分，在几何学的许多不同领域都很重要。
• 几何模型的构建，特别是多面体等三维结构，是对顶角的另一个重要应用。数学家可以通过利用对顶角的特性来设计精确且美观的几何模型。这对于设计、工程和建筑等各个行业具有重要意义。
• 为了解决涉及角度的代数方程，对顶角也至关重要。例如，如果我们知道两个角是对顶角并且我们知道其中一个角的度数，我们可以使用对顶角定理来确定另一个角的度数。这有助于解决物理和工程等学科中出现的涉及角度的代数方程。
• 角度及其与其他三角形边和角度的关系也是三角恒等式的一部分。可以使用对顶角的特性来证明三角恒等式并推导出新的恒等式。这在天文、测量和导航领域具有重要用途。
• 此外，在实际应用中测量角度需要使用对顶角。工程师和建筑师使用对顶角来建造建筑物和其他结构。

天文学家使用对顶角来研究天体的位置和运动，而测量员使用它们来计算距离和高度。这些用途突出了对顶角在与我们日常生活直接相关的各种领域中的关键作用。

总而言之，对顶角在各种数学和科学学科中都有许多重要用途。在实际环境中，它们用于证明几何定理、构建几何模型、解决代数问题、证明三角恒等式和测量角度。理解许多基本数学和科学主题需要理解对顶角的特性和用途。

结论

总而言之，掌握对顶角的概念对于理解各种关键的数学和科学主题至关重要。对顶角在两条线相交时产生，并且总是全等的、彼此相对并共享一个顶点。它们还具有其他基本性质，例如互补并与相邻角形成一种线性对。

对顶角的一个重要性质是对顶角定理，该定理指出当两条线相交时形成的对顶角总是全等的。该定理在几何学、代数、三角学和相关学科中有许多重要应用。它可用于建立其他定理、解决代数问题和设计几何模型。

对顶角的另一个主要应用是建筑物和结构的设计和建造。建筑师和工程师利用对顶角来生成精确的设计并确保其项目的结构完整性。测量员利用对顶角来测量距离和高度，而天文学家则利用它们来研究天体的位置和运动。

对顶角在数学和科学模型的构建中也起着关键作用。它们帮助我们理解和描述自然现象和物理宇宙的行为。如果不理解对顶角，就不可能创建有效反映不同变量之间复杂相互作用的模型。

此外，对顶角的研究有助于我们理解二维和三维形状和角度的性质。这种理解在工程、建筑、物理和几何等学科中至关重要。它还使我们能够解决现实世界中的实际挑战，例如创建结构和测量距离。

总的来说，对顶角在各种数学和科学领域中具有众多重要应用。它们在描述自然事件的模型开发中起着关键作用，并且是建筑物和结构设计和建造的基础。理解对顶角对于解决工程、物理和几何等领域的问题也至关重要。总之，对顶角是数学和科学中的一个基本概念，它们的研究对于理解许多基本概念和应用是必不可少的。