梯形定义

虽然梯形在数学中是一种多边形，但在日常生活中很少使用。尽管如此，在现实中可以找到几种模型。接下来的部分将介绍梯形的定义、公式、属性和示例。

与任何其他数学对象一样，梯形是一种属于四边形类别的多边形。要理解梯形，必须首先理解是什么使其成为四边形。梯形是四边形，因为它有四条边在四个不同的点相交，以及四个顶点。因此，梯形表现出四边形的所有特征。

梯形与正方形或方形不同，因为它只包含一对相似的线。这意味着梯形只有两条相对的边是平行的。

梯形的相等边称为其**底**，而非相等边称为其**腰**。梯形有时被称为**梯形（trapezoid）**。然而，这两种图形并不相似。

梯形的形状

梯形与其他二维形状一样，有两层。无论如何，梯形由四条直线组成，这些直线连接形成四个不同的点。虽然正方形和方形包含两对相似的线，但梯形只有一对相似的线是相对流动的。

梯形与大多数多边形一样，有四条边和四个角。该图形由两条相对的平行线表示。这种形状可以看作是一张上面是梯形的桌子。

梯形的性质

• 梯形是一个两层形状。
• 梯形的一对相对边与另一对对齐。
• 这些平行线称为底。
• 梯形的一组相对边不平行。
• 这些不等边称为梯形的腰。
• 梯形的对角线长度相等。
• 在梯形中，斜线和平行线都会相互交叉。
• 梯形的连续内角和为 180°。

梯形的公式

梯形是我们身边常见的形状中独一无二的。要理解梯形的各种方程，需要了解其结构。以下是一个梯形。

理解梯形的形状将更容易理解其面积和周长公式。

梯形的面积由下式给出

梯形的面积 = [(AB + DC)/2] h

此处，

AB 表示底 a 的长度。

DC = 底 b 的长度

h = 梯形的高

梯形的周长是图形所覆盖的边界的总长度。因此，**梯形的周长**等于边 AB + BC + CD + DA 的总和。

梯形有哪些不同类型？

根据梯形不同的结构和性质，它们被分为三种重要类型。三种基本的梯形类型是

• 等腰梯形
• 不等边梯形
• 直角梯形

梯形有三种不同的形状，但它们都具有相同的特征。这意味着上述每种梯形都有一对相对的平行边。

1. 等腰梯形

在梯形中，非等边称为腰。如果梯形的腰长度相等，则称为等腰梯形。

2. 不等边梯形

梯形是四边形。它有四条边组成不同的点。然而，不等边梯形四条边的测量值和点并不非常相似。因此，它被称为不等边梯形。

3. 直角梯形

直角等于 90°。因此，在直角梯形中，两条非等边相邻形成两个直角。因此，它是一个直角梯形。

梯形的周长

图形的周长被认为是图形的总边界长度，在这种情况下，梯形的周长等于梯形四条边各自的长度。

要计算梯形的周长，首先必须知道梯形四条边各自的长度。通过知道四条边的测量值，可以组合这些特征来确定周长。

例如，假设一个梯形有四条边，分别是 12cm、13cm、14cm 和 18cm。那么，它的周长将是 -

12 + 13 + 14 + 18 = 57 毫米 梯形周长

如何计算和求梯形的面积？

面积被定义为图形所包围的总范围。因此，梯形的面积被建议为梯形四条边所包围的总空间。

例如，梯形的相等边是 - 8 厘米和 6 厘米。它们之间的距离是 - 10 厘米，那么面积由下式给出：

= [(8 + 6)/2] × 10

= [14/2] × 10

= 7 × 10

梯形面积 = 70 cm²

什么是梯形（Trapezoid）？

梯形（Trapezoid）是一个平面、封闭的图形，有四条直线边和一对相等的边。

梯形（Trapezium）的相等边是其底，而非相等边是其腰。梯形（Trapezium）也可以有相等的腰。相等边可以是水平、垂直或倾斜的。相等边之间的垂直距离称为高。

梯形（Trapezium）与梯形（Trapezoid）有何不同？

在许多情况下，梯形（Trapezium）会与梯形（Trapezoid）混淆。

为避免混淆，请记住，梯形（Trapezium）是一个四边形。也就是说，它有四条边形成四个不同的角度。而梯形（Trapezoid）则没有任何平行线。

什么是不等梯形？

在不等梯形中，一对相等线会相交。然而，在不等梯形中，没有相等的边。这意味着四条边彼此不平行。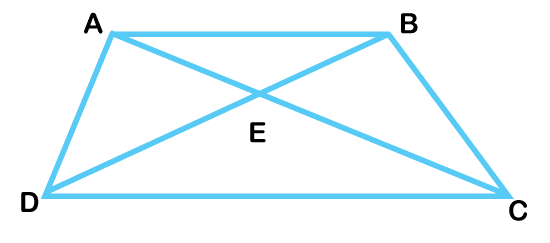

不等梯形也不满足梯形的性质。尽管它也是四边形，但它没有一对相对的平行线。

梯形的对角线可以互相平分吗？

人们普遍误认为梯形的对角线会互相平分。但这是不正确的。

答案是梯形的对角线不会互相平分。此外，平行四边形的对角线会互相平分。假设每两个梯形中只有一个是平行四边形。然而，每个平行四边形都是梯形。

结论

梯形是一种四边形的封闭图形，具有一对相互平行的边和一对不相等的边。它是一个有四条边、四个角和四个顶点的四边形。所有内角之和为 360 度。相邻边之间的角度为 180 度，并且该构造的对角线会分开。梯形的底是其限制性的平行边之一。有趣的是，梯形的高是两条平行线之间的垂直距离。