Excel 中的线性规划2025年3月17日 | 阅读 7 分钟 本教程演示了如何使用 Excel 解决整数线性规划问题。借助 Microsoft Excel 中的“规划求解”加载项,用户可以快速找到整数线性规划的解决方案。今天,我们将通过简单明了的步骤完成此过程。本教程的最后一部分还将看到一个混合整数线性规划问题的示例。所以,让我们立即开始。 整数线性规划整数线性规划使用整数变量、线性目标函数和方程。在特定条件下,可以使用线性规划找到特定问题的最小或最大结果。它是一种可用于找到使用稀缺资源的最有效策略的工具。所有形式的线性规划都有几个关键组成部分。以下是它们的详细信息 - 决策变量:我们确定哪些选择将减少或最大化目标函数。
- 目标函数:目标函数有助于我们识别决策变量。它传达了变量和结果之间的关系。
- 约束:约束是附加函数,表示潜在解决方案的各种要求。
除了整数线性规划之外,还将展示一个混合整数线性规划示例。混合整数线性规划中存在连续变量和整数变量。 Excel 解决整数线性规划的分步说明我们将使用一个示例来演示分步方法。要理解基本概念,您必须仔细阅读。您必须仔细阅读问题并确定目标函数和约束。 假设一台机器生产两种可互换的商品。该机器每天最多可生产 20 单位的商品 1 和 10 单位的商品 2。另一个选择是将机器设置为每天最多生产 22 单位的商品 1 和 18 单位的商品 2。根据市场分析,两种商品的总日需求量为 40 单位。在两种机器设置之间进行选择时,如果两种商品的单位利润分别为 15 美元和 18 美元,应该选择哪种? 步骤 1:检查问题并建立数据集- 首先,我们必须充分理解并彻底检查所提供的整数线性规划问题。
- 上述查询的分析结果如下所示。
决策变量 - X1:产品的生产数量
- X2:产品 2 的生产数量。
- Y:如果选择第一种设置,则为 1;如果选择第二种设置,则为 0。
目标函数 在这种情况下,目标函数是 约束 上面的问题主要导致我们有三个限制。它们是 根据市场分析,两种商品的总日需求量最大为 40 单位。 对于产品 1,只有此约束适用。 对于第二种产品,它是一个限制。 Y 将为零或一。 产品数量不能为负。 - 考虑到约束、函数和变量,我们在后续步骤中生成了一个数据集,如下图所示。您可以根据需要修改它。
 步骤 2:打开 Excel 并加载规划求解加载项- 其次,我们必须打开 Excel 并加载规划求解加载项。如果数据已在 Excel 中,您可以继续执行步骤 3。
- 单击“文件”选项卡即可完成此操作。
 - 接下来,单击屏幕左下角的“选项”。
- 结果将打开“Excel 选项”。
 - 从“Excel 选项”窗口中选择“加载项”。
- 接下来,在“管理”框中,选择“Excel 加载项”,然后单击“转到”。
- 将显示一个关于加载项的消息框。
 - 选中“规划求解加载项”后,从通知框中选择“确定”。
 - 最后,您可以在“数据”选项卡的“分析”部分下看到“规划求解”功能。

步骤 3:填写目标函数和约束系数- 第三,必须填写数据集的目标函数和约束。
- 我们主要在此处插入目标函数和约束系数。
- 2X1+3X2<=40 是我们的初始约束。这表示如果使用初始设置,产品的总量应等于或小于 40。
- X1 和 X2 的系数分别为 2 和 3。
- 此外,Y 的系数为 1,因为方程显示了初始配置。
- 它有一个<=符号。
- 此外,40是上限。
 - 再次按照之前的说明,输入每个约束的系数。
 - 接下来,选择单元格D10并输入以下公式
 此公式使用 SUMPRODUCT 函数来计算决策变量与相关约束变量的乘积,然后将其相加。单元格 A6 将乘以单元格 A10,单元格 B6 将乘以单元格 B10,单元格 C6 将乘以单元格 C10。随后,每个乘积将合并。 - 按 Enter 并拖动填充手柄。
 - 现在,用目标函数的系数填充单元格 A16 到 B16。
- Z = 6X1+8X2 是我们场景中的目标函数。
 - 再次选择单元格 D16,然后输入以下公式
 - 输入系数和公式后,按 Enter 即可查看如下图所示的数据集。

步骤 4:输入规划求解的参数- 步骤 4 涉及从“数据”选项卡下的“分析”部分选择“规划求解”。将打开规划求解参数窗口。
 - 您必须在“设置目标”框中输入包含目标函数值的单元格。
- 因此,我们在此处输入 $D$16。
- 在这种情况下,我们的目标是最大化结果。
- 在“通过更改可变单元格”中键入 $A$6:$C$6,其中包含用于做出决策的变量。

步骤 5:添加受约束- 在第五阶段,必须将主体添加到约束中。
- 必须指明限制与变量类型(二进制或整数)之间的关系。
- 因此,请选择“添加”。将显示“添加约束”对话框。
 - 在“添加约束”对话框的“单元格引用”框中键入 $C$6 后,使用下拉选项选择“二进制”。
- Y 为 0 或 1。单元格 C6 包含此值。它表示二进制数。我们选择此特定二进制数的原因。
- 单击“确定”继续。
 - 再次选择“添加”。
 - 这次,在“单元格引用”框中填写 $D$10:$D$12,通过下拉菜单选择“<=”符号,然后在“约束”框中输入 =$F$10:$F$12。
- 接下来,按“确定”。
 - 从“规划求解参数”窗口中,再次单击“添加”。
 - 现在将 $A$6:$B$6 输入到“单元格引用”字段中,并在下拉列表中选择“整数”。
- 整数 X1 和 X2 的值存储在单元格 A6 和 B6 中。
- 再次按“确定”。

步骤 6:选择求解方法- 在步骤 6 中,当提示“选择求解方法”时,选择“单纯形 LP”并按“求解”。
- 应选中“使无约束变量非负”。
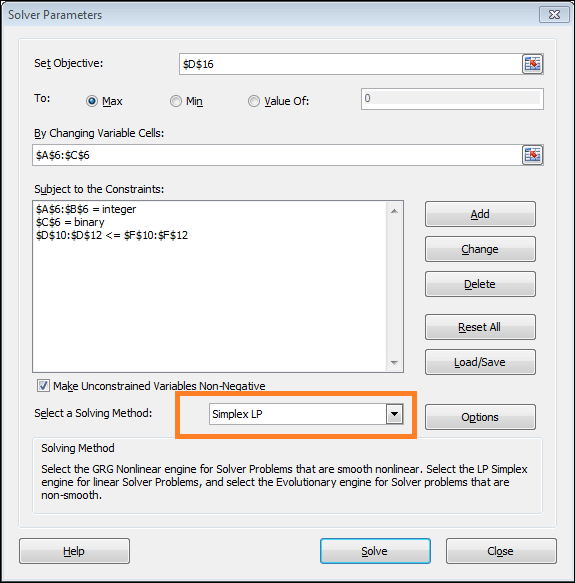 - 选择“求解”后,将打开“规划求解结果”窗口。
- 之后,选择“确定”。

步骤 7:整数线性规划解决方案- 在 Excel 工作表中,您最终将在所需的单元格中找到解决方案。
- 在这种情况下,我们将使用第二台机器选项获得最大的结果。
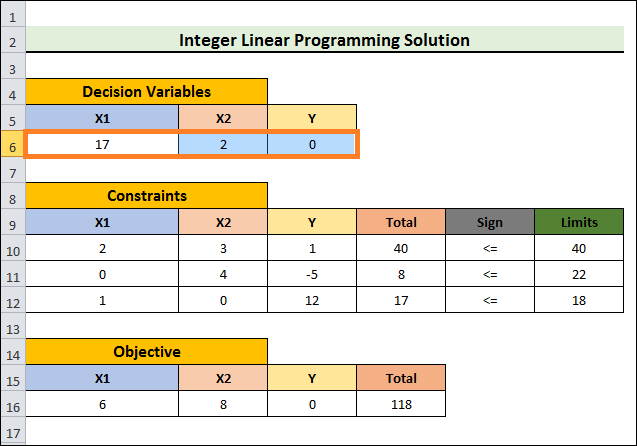
步骤 8:创建答案报告- 您还可以生成响应报告。
- 从“规划求解结果”框的“报告”区域中选择“答案”,然后单击“确定”即可完成此操作。
 - 该报告最终位于另一个工作表中。

Excel 中混合整数线性规划的示例本部分将讨论一个简单的 Excel 混合整数线性规划示例。使用 Excel 解决混合整数线性规划的简单步骤如下。让我们在此场景中检查目标函数及其相应的约束。 目标函数 - Z = 2.52X1+1.55X2+2.55X3 + 250Y1 + 300Y2 + 400Y3
约束 - X1-350Y1<=0
- X2-400Y2<=0
- X3-450Y3<=0
- X1+X2+X3=1000
在此实例中,变量 X1、X2 和 X3 是整数。然而,Y1、Y2 和 Y3 是二进制数。我们还需要确定 Z 的最小值。 让我们执行下面列出的步骤,以了解有关该示例的所有信息。 步骤 - 构建一个数据集来保存决策变量、约束和目标函数系数。
 - 其次,查找目标函数变量的混合系数。
 - 第三,输入约束变量的系数,如下图所示。将“总计”列留空。
 - 接下来,选择单元格G10并输入以下公式
 - 要删除填充手柄,请按Enter。
 - 现在在单元格G6中输入以下公式
- 按Enter。
 - 转到“数据”选项卡,然后在下一步中选择“规划求解”。结果将打开“规划求解参数”窗口。
 - 通过调整变量单元格 $A$6:$F$6,在“规划求解参数”窗口中将单元格 $G$6 中的目标设置为最小值。
 - 之后单击“添加”。
 - 逐个添加约束,并为求解方法选择“单纯形 LP”。
- 如需进一步操作,请单击“求解”。
 - 然后将弹出“规划求解结果”窗口。
- 接下来,单击“确定”。
 - 结果最终将如下图所示。

| 


