二维图形

二维（或三维）图形可以定义为可以在坐标系中绘制的几何图形，由 X 和 Y 平面组成。它与三维图形不同之处在于，二维图形的每一点始终由两个坐标（X, Y）组成。

二维图形是可以在纸上或平面上绘制的平面图形。一些二维图形有角和边，而一些则有曲线边界。具有曲线边界的二维图形是圆和椭圆。

一些基本的二维图形的例子包括圆、矩形、三角形、正方形、八边形、五边形等。除了圆、椭圆和其他具有曲线边界的二维图形外，所有图形都被认为是多边形。多边形是表面的表示。它是原生的，封闭的。它由一组线段形成。它也被称为多边形。构成多边形的线段称为边。线段通过组合两个顶点获得。

让我们通过图像来讨论基本的二维图形及其表示。我们还将讨论它们的重要公式。

圆

圆是具有与中心相同距离并连接到其起始点的曲线。换句话说，它是所有到原点距离相等的点的轨迹。圆的例子有车轮、硬币、光盘等。它是一个圆形图形。我们可以在下图看到圆的表示 -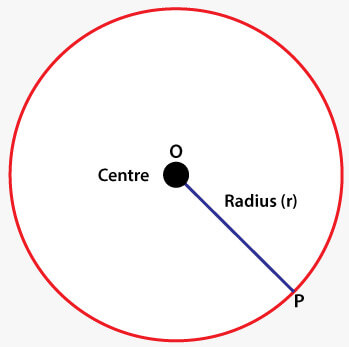

圆包含各种部分，如直径、半径、周长、圆心、切线等等。圆的类型包括切线圆、同心圆和全等圆。一些常用的圆的公式如下 -

圆的面积 (A) = πr²

直径 (d) = 2 × 半径 (r)

半径 (r) = 直径/2

周长 (C) = 2πr

矩形

矩形是一种二维图形，包含四条边，其中相对的边平行且相等。矩形是具有两对相等边和四个直角的几何图形。矩形是一个有四条边的多边形。矩形的性质是相对边的长度必须相等。我们可以使用包含长和宽的公式来计算矩形的面积。

矩形的例子是砖块、纸板等。我们可以在下图看到矩形的表示 -

计算矩形面积的公式等于矩形的长乘以宽。

矩形面积 (A) = 长 × 宽

Square

正方形是二维平面上的闭合图形，具有四条平行且相等的边。正方形的性质是所有边（宽和长）的长度必须相等。在正方形中，每个角都是 90°。正方形的表示如下图所示 -

计算正方形面积的公式如下 -

正方形面积 (A) = a × a

或者，

正方形面积 (A) = (a) ²

其中 a 是正方形的边长。

三角形

三角形是具有三个顶点和三条边的多边形。三角形的三个内角之和为 180 度。三角形有各种类型，如等边三角形、等腰三角形、不等边三角形、锐角三角形等。每种类型都有其自身的性质，但共同点是它们都有三条边，并且它们的内角之和等于 180 度。三角形最好的例子是金字塔。

三角形的表示如下图所示

计算面积的公式对于不同类型的三角形可能有所不同。三角形的面积是三角形所覆盖的区域。三角形的面积等于底乘以三角形的高的一半。

如果给定的三角形是直角三角形，则将两条与直角相邻的边相乘。

这里，我们讨论两种计算三角形面积的公式。计算三角形面积的公式如下 -

1. 它是底乘以高的一半。下面的公式适用于所有三角形。

三角形面积 (A) = ½ × b × h

其中 b 表示底，h 表示给定三角形的高。

2. 海伦公式也可用于计算三角形的面积。但当给出三角形的所有边或所有三条边都不相等时，才能使用。

三角形面积 (A) = √(s(s-a)(s-b)(s-c))

其中 a, b, c 是三角形的边，s 是半周长，计算方法如下 -

半周长 (s) = (a + b + c) / 2

可以根据不同的性质有其他计算三角形面积的公式。

平行四边形

平行四边形可以定义为一种四边形（四条边）形状，具有两对平行线。相对的边和全等的角测量相等。平行四边形的内角之和为 360°。平行四边形的特殊类型包括菱形、正方形、矩形和斜方形。

平行四边形的表示如下图所示 -

平行四边形的相对边和角是全等的。计算平行四边形面积的公式与矩形相同。这是因为平行四边形可以转换为矩形。

要计算平行四边形的面积，将底乘以高，反之亦然。换句话说，平行四边形的面积是底乘以高。

平行四边形面积 (A) = 底 (b) * 高 (h)

梯形

梯形是凸四边形。这意味着它是一个具有四条边和一对平行边的封闭图形。

梯形（也称为梯形）是一种包括四条边的几何形状，其中一对相对的边是平行的。平行边称为底，非平行边称为腿。平行边可以是水平的、垂直的或倾斜的（对角的）。

梯形的表示如下图所示 -

计算梯形面积和周长的公式如下 -

梯形面积 (A) = ½ (b1 + b2) * h

或者，

梯形面积 (A) = h/2 * (b1 + b2)

或者，

梯形面积 (A) = h * (b1 + b2/2)

梯形周长 = 所有边之和 = AB + BC + CD + DA