年有效利率公式

年有效利率（AEIR）是金融领域的一个基本概念，它在考虑复利的情况下，能可靠地评估金融产品的年度成本或回报。当复利每年发生多次时，AEIR 就能真实反映货币的实际回报或成本，而名义利率则无法考虑复利频率。因此，AEIR 是评估各种金融产品更准确、更实用的指标。

AEIR 实际上回答了“如果复利只发生一次，那么等效的年利率是多少？”这个问题。在评估投资的实际盈利能力、贷款成本以及其他经常发生复利（如每月或每天）的金融工具时，它尤其有用。

在日常决策和理财中，AEIR 至关重要。例如，通过进行同类比较，AEIR 使人们在评估贷款优惠或储蓄账户时能够做出明智的决定。为了确保客户了解其金融交易的实际成本或收益，金融机构也将其作为透明度的标准指标。

通过了解 AEIR，企业和个人可以做出更明智的财务决策，从而确保他们能够最大限度地减少借贷成本或最大限度地提高投资利润。它是金融素养的基本工具，让消费者有信心成功驾驭复杂的金融市场。

利率

利率对金融至关重要，它代表着借贷的成本或储蓄的好处。名义利率是指金融产品（如贷款或储蓄账户）上规定的利率，但不考虑复利的影响。例如，一笔贷款可能宣传其名义年利率为 12%，这表明在一年内使用的是简单利率。

然而，名义利率并不总是能准确反映实际成本或收益。这时，有效利率（EIR）就显得尤为重要了。EIR 考虑了一年内的复利频率，提供了一个更精确的实际支付或赚取利息的衡量标准。例如，当 12% 的名义利率按月复利时，EIR 会增加，因为利息是在每个月已添加到本金上的利息基础上计算的。

名义利率和有效利率的区别在于复利。尽管名义利率保持不变，但 EIR 随着复利频率的增加而增长。一个实际的例子可以说明这一点：信用卡可能提供 24% 的名义年利率，但如果按日复利，有效利率（EIR）或年化利率（APR）可能会超过 26%。同样，提供 5% 名义年利率且按季度复利的储蓄账户，其 EIR 会超过 5%。

年有效利率公式

年有效利率（AEIR）提供了一个精确的评估，用于衡量一年内金融产品所获得的或支付的实际利息，并考虑了复利的影响。

计算 AEIR 的公式为

其中

• i：名义年利率（以小数表示，例如 5% = 0.05）
• n：每年复利次数（例如，每月复利为 12）

该公式通过承认复利在一年内按固定间隔发生，从而计算出有效利率。每个复利期都包含原始本金的利息以及已计入的利息，这使得 AEIR 成为实际成本或回报的更精确的表示。

例如，考虑一笔名义年利率为 12%，每月复利的贷款。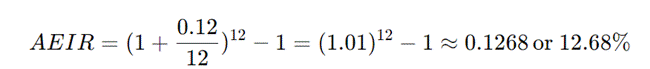

这意味着，实际上，借款人面临的年利率为 12.68%，而不是声明的名义利率 12%。

AEIR 在评估具有不同复利期的金融产品时尤其重要。例如，年利率为 5% 且按季度复利的储蓄账户，其 AEIR 会高于相同利率但按年复利的储蓄账户。

AEIR 计算

让我们通过一个例子，一步一步地计算年有效利率（AEIR），以更好地理解其运作方式。假设一家银行提供三种不同的复利频率：每年、每月和每天，名义年利率均为 10%（i = 0.10）。

步骤 1：理解公式

AEIR 公式为

其中

• i：名义年利率
• n：每年复利次数

步骤 2：计算每种复利频率

每年复利（n=1）

每月复利（n=12）

每日复利（n = 365）

AEIR 随复利频率的增加而增加。这是因为更频繁的复利增加了总利率，因为它允许利息更频繁地计入以前赚取的利息。

步骤 3：比较结果

步骤 4：解读结果

随着复利频率的增加，AEIR 也随之增加。这是因为更频繁的复利允许利息更频繁地计入以前累积的利息，从而提高了总利率。

AEIR 的应用

AEIR 帮助投资者确定债券、定期存单（CD）和储蓄账户等投资的实际回报。例如，一家宣传按季度复利 6% 名义回报的投资，其 AEIR 可能为 6.14%。投资者因此可以有效地比较各种选项，最大限度地提高他们的利润。

贷款比较

由于 AEIR 提供了一个一致的指标来评估金融产品，因此它对长期财务规划至关重要。人们可以利用 AEIR 来预测准确的增长或成本，无论是为大额支出进行储蓄还是规划退休，从而使他们能够做出更符合其财务目标的明智决策。

投资分析

对于债券、定期存单（CD）和储蓄账户等资产，AEIR 帮助投资者确定其资金的实际回报。例如，一项提供按季度复利 6% 名义回报的投资，其 AEIR 可能为 6.14%。这种透明度使投资者能够有效地比较各种选项，增加他们的收益。

财务规划

AEIR 对长期财务规划至关重要，因为它提供了一个评估金融产品的标准指标。在为大额购买做准备或制定退休计划时，人们可以使用 AEIR 来预测准确的增长或成本估算，这有助于他们做出更符合其财务目标的明智决策。

现实生活场景

想象一下，一位房主正在评估两个抵押贷款方案：一个提供 4% 的名义月复利利率，另一个提供 4.2% 的名义年复利利率。虽然第一个方案看起来更便宜，但房主可以通过计算 AEIR（它显示了实际费用）来选择更优的方案。同样，AEIR 也可以帮助年轻专业人士评估高收益储蓄账户，以确定其真实价值。

AEIR 的优势和局限性

作为金融领域的一个有用工具，年有效利率（AEIR）具有许多优势。由于它考虑了复利，因此它准确地反映了金融产品的成本或回报，这是其主要优势。因此，AEIR 比名义利率更准确，特别是对于经常复利的产品。此外，AEIR 促进了可比性，使个人和组织能够对金融产品进行一致的评估，尽管复利期不同。在比较投资账户、抵押贷款或贷款时，AEIR 提供了一个一致且透明的指标。

然而，AEIR 并非没有局限性。它假设复利恒定，这并不总是与实际情况相符，这是一个主要缺点。例如，在某些金融产品具有浮动利率或不规则复利计划的情况下，AEIR 的可靠性较低。此外，AEIR 没有考虑可能影响总成本或回报的其他变量，例如费用、通货膨胀或提前还款罚金。

尽管存在这些缺点，AEIR 在比较具有规律复利和固定利率的金融产品时仍然非常有用。当满足这些要求时，它非常适合评估投资产品、固定利率贷款和储蓄账户。另一方面，对于浮动利率产品或条款不规则的产品，诸如年化利率（APR）或总借款成本等其他指标可能更合适。

高级注意事项

尽管年有效利率（AEIR）是大多数金融比较的有用工具，但像连续复利和外部经济因素这样的复杂概念使其应用更加困难。

连续复利是一种极端情况，其中利息在指定的时间段内无限期地复利。在连续复利中的有效利率可以使用以下公式计算

在这种情况下，i 是名义年利率，而 e 是数学常数，约为 2.718。连续复利的有效利率略高于每日复利的有效利率。例如，在 10% 的名义利率下，连续复利的 AEIR 大约是 10.52%，而每日复利的 AEIR 是 10.51%。尽管差异很小，但在高频交易、衍生品定价和其他复杂的金融情况中，这种差异变得很重要。

外部因素，如风险和通货膨胀，也会影响 AEIR 的有用性。由于通货膨胀会降低回报的购买力，因此实际有效利率可能低于 AEIR。同样，可能需要进行调整以反映金融工具的实际成本或回报，因为风险因素（如信用worthiness 或市场波动性）会影响这些因素。

通过考虑复利，年有效利率（AEIR）这一关键的财务指标，对经济商品的实际成本或回报提供了精确的评估。本文探讨了 AEIR 的定义、公式、计算方法和现实世界中的应用，强调了它如何能够使贷款、投资和储蓄的比较更易于理解。我们还讨论了其优点、缺点以及更复杂的因素，如通货膨胀和连续复利。

理解 AEIR 对于做出明智的财务决策至关重要。无论是在最大化投资回报还是评估借贷机会时，AEIR 都为个人和组织提供了一个一致且清晰的利率衡量标准。

在您的财务旅程中，请利用 AEIR 批判性地评估您的选择。通过这样做，您可以改善您的财务状况，做出更好的决定，并获得更多的财务信心和清晰度。