标准分布图

在统计学中，一种常见的图表类型，称为正态分布或钟形曲线，是一个重要的概念。它是一种图形表示，显示数据在以均值为中心的各种值上的分布情况。该图表显示了对称性，表示围绕平均值的镜像形状，形成一个类似于钟形的曲线。标准分布图的重要性在于它能够帮助统计学家识别数据模式并进行预测。由于许多现实生活中的事件自然地遵循这种分布模式，因此它经常被用于经济学、心理学和自然科学等各个领域。理解钟形曲线对于正确解释数据和在统计分析中做出明智的选择至关重要。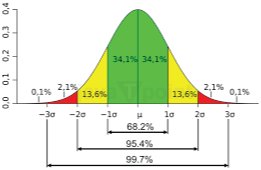

什么是标准分布图？

普通分布图，通常称为钟形曲线，说明了数据点的分布情况。钟形曲线的名字来源于其像钟一样的形状。这种形状是由数据点集中在中间值而产生的，随着与中心的距离增加而减少。

图表的中间点对应于平均值，即所有数据点的总和除以数据点的数量。在典型分布中，平均值、中位数和最频繁值都恰好在图表的顶部。图表的对称性是一个重要的特征，左侧反映右侧。这种平衡表明数据在平均值周围均匀分布。

理解数据如何表现至关重要，因此标准分布 图很重要。例如，在大量数据（如考试成绩）中，大多数人将获得接近平均分数的成绩，而很少有人能获得非常高或非常低的分数。这种容易预测的模式使我们能够做出更准确的预测并更有效地分析数据。在统计学中，对钟形曲线有很好的掌握至关重要，因为许多自然和社会现象都遵循这种分布。

标准分布图的关键组成部分

典型的分布曲线，也称为高斯分布，包含几个有助于数据解释的重要组成部分。这些包括平均值、离散度、Z分数和百分位数，所有这些对于检查分布都至关重要。

• 平均值（Mean）：平均值代表数据集的典型值。大多数数据在此点附近集中，并且在典型分布图中，平均值位于峰值。这使其成为理解完整数据模式的重要来源。平均值至关重要，因为它象征着数据集中通常的值。
• 标准差（Standard Deviation）：标准差衡量数据集的值相对于平均值的分布范围。当大部分数据点集中在平均值附近时，会产生一个狭窄而尖锐的钟形曲线，这由较低的标准差显示。另一方面，较高的标准差表示数据点分布更广，导致曲线更宽、更浅。理解标准差至关重要，因为它表示数据的变异性。
• Z分数（Z-Scores）：Z分数利用标准差来衡量与平均值的距离。Z分数为 0 表示该值恰好在平均值上，而正 Z 分数或负 Z 分数表示其与平均值的标准差数量，无论是高于还是低于。Z分数很有用，因为它们可以标准化数据点以便在分布内部或之间进行比较。
• 百分位数（Percentiles）：百分位数显示特定值在分布中的位置。当位于第 80 百分位数时，这意味着 80% 的数据点低于该特定值。通过分析图表中位于特定值左侧的区域来确定百分位数。这个概念在教育评估或任何需要了解某个值与他人相比的重要性的情况下都很有价值。

标准分布的应用

钟形曲线，也称为标准分布，由于其能够准确地以自然方式描绘数据分布的能力，因此在不同领域得到了广泛应用。其广泛用途主要在研究、商业和教育领域。

• 在研究中：科学家依靠正态分布进行 数据分析和推断。由于许多自然现象的正态分布，该图表有助于研究人员理解模式和进行预测。在社会科学中，研究人员可以利用它来检查调查结果，验证数据与预期模式的一致性，并简化异常检测。
• 在商业中：在商业世界中，公司出于各种目的实施正态分布，包括市场分析和质量控制。公司通过分析购买模式来分析客户行为数据进行市场分析，以预测即将到来的趋势并做出明智的决定。制造商在质量控制中使用钟形曲线来监督产品质量。通过绘制产品尺寸或错误频率等信息，他们能够评估一个过程是否可靠并且在可接受的范围内，从而确保产品符合质量标准。
• 在教育中：在教育领域，正态分布在标准化测试和评分中至关重要。考试成绩通常符合钟形曲线，大多数学生获得的成绩接近平均值，而少数学生获得非常高或非常低的分数。教师利用这条曲线进行评分，将平均分数设定为 C 等级，并相应地调整其他分数。这种方法确保评分是公正的，并准确地代表了小组的整体成就。

如何创建标准分布图

生成标准分布图是一项简单的任务，可以使用 Excel、Python 或专用的统计 软件等工具完成。这是一个详细的指南，可以帮助您绘制图表。

步骤：

• 收集数据：从您想要检查的数据集开始。这可能包括从考试成绩到科学研究中的测量。
• 确定平均值和标准差：平均值代表数据集的平均值，而标准差表示数据点偏离平均值的程度。创建平均分布图需要这些计算。
• 生成数据范围：为了生成图表，您必须创建一个涵盖数据集的值集。此区间通常包括比平均值低几个标准差到比平均值高几个标准差的值。
• 绘制图表：使用您选择的工具创建可视化表示来绘制图表。在 Excel 中，您可以使用内置函数来计算数据集中每个值的正态分布。接下来，在 x 轴代表数据范围，y 轴代表计算出的正态分布的图上绘制这些值。

工具

• Excel：Excel 因其易用性和可访问性而被广泛使用。它包含简化平均值、标准差和高斯分布计算的功能。
• Python：Python 为高级用户提供了 Matplotlib 和 NumPy 等强大的库，这些库可以有效地处理复杂的计算和大型数据集。
• 统计软件：SPSS 或 R 等统计软件专为统计分析而设计，可以简化传统分布图的生成过程。

示例

一旦您计算出平均值和变异性，您就可以使用 Excel 创建一组分数以及它们各自的平均分布值。当绘制在图表上时，您会注意到典型的钟形曲线形状，大多数学生得分接近平均值，而少数学生得分非常高或非常低。

解释标准分布图

在解释标准分布图时，理解钟形曲线的形状和含义至关重要。该图表说明了数据分布并有助于进行预测，但准确的解释对于避免常见错误至关重要。

• 理解分布和偏度：通过观察标准分布曲线的形状，您可以深入了解您的数据。在完美的正态分布中，图表显示对称性，在平均值处达到峰值。受标准差影响的图表范围表示数据变化的程度。更宽的分布表示更多样性，而更紧凑的分布表示数据点更接近平均值。有时，图表可能不对称，表明朝着一个方向偏斜。正偏斜表示存在一些异常高的值，而负偏斜表示存在低值。偏斜会影响对数据平均值和分布的解释。
• 进行预测：标准分布图的一个关键应用是进行预测。通过检查可视化表示，可以通过观察曲线的模式来预测未来的数据点。知道大多数值落在平均值的一个标准差范围内，这表明预计未来的数据点也将在此范围内。这在多个领域都很有价值，例如预测学生的成绩或预测公司的未来利润。
• 常见误解：解释平均分布图时可能会出现错误。一个常见的错误是期望每个数据集都完美符合正态分布，但这并不总是真的。现实世界中的实际数据有时可能比完美的钟形曲线表现出更多的离散度或不对称性。另一个错误是未能考虑异常值，即不符合预期模式的数据点。如果不考虑这些因素，它们会扭曲您的理解。最后，人们有时会误解图表，仅仅关注平均值而忽略了离散度，导致对数据变异性做出不准确的推论。

结论

总之，理解标准分布图对于分析研究、商业和教育等各个领域的数据至关重要。这些图表帮助我们可视化数据模式，进行预测，并得出有意义的结论。通过掌握均值、标准差和曲线形状等关键概念，您可以更有效地解释数据。对于有兴趣深化知识的人来说，探索统计教科书或使用 Excel 和 Python 等工具进行练习非常有益。