海伦公式17 Mar 2025 | 5 分钟阅读 海伦公式也称为英雄公式。它以希腊裔埃及工程师和数学家亚历山大港的海伦的名字命名。当已知三角形的三条边时,它用于计算三角形的面积。 海伦公式由以下公式给出:  或  其中, S = 三角形的半周长 它由s = (a + b + c) /2给出 半周长:之所以称为半周长,是因为它的值是一个三角形周长的一半。周长定义为给定图形所有边的总和。对于三角形,周长等于其三条边的总和。 变量 a、b 和 c 是三角形的边。 海伦公式与其他公式不同,因为它不需要任何角度测量。 我们也可以用三角形的边来写公式。我们需要在公式中使用 s = (a + b + c) /2。 它由下式给出  上面的公式也是海伦公式,但没有半周长 (s)。它用三角形的三条边 (a, b, 和 c) 来表示。 实际问题让我们通过一些与海伦公式相关的实际问题来解决。 示例 1:求边长为 a = 4m、b = 5m 和 c = 3m 的三角形的面积。 解决方案 三角形半周长 = s = (a + b + c)/2 S = 4 + 5 + 3/2 = 12/2 = 6m 三角形面积 A = (6 (6 - 4) (6 - 5) (6 - 3))^1/2 A = (6 x 2 x 1 x 3)^1/2 A = (36)^1/2 A = 6m^2 因此,三角形的面积是 6 平方米。 示例 2:求三角形的面积,如果三角形的两条边是 4m 和 3m。三角形的半周长是 5m。 解:在这里,我们将首先使用半周长公式找到三角形的第三条边。之后,我们将计算三角形的面积。 我们知道, S = (a + b + c)/2 5 = (4 + 3 + c)/2 5 x 2 = 4 + 3 + c 10 = 7 + c 3 = c 因此,三角形的第三条边是 3 厘米。 三角形面积由以下公式给出:  A = [5 (5 - 4) (5 - 3) (5 - 3) ]^1/2 A = [5 x 1 x 2 x 2] ^1/2 A = (20)^1/2 A = 4.47 平方米 因此,三角形的面积是 4.47 平方米。 示例 3:求边长为 4m 的等边三角形的面积。 解:等边三角形的三条边相等。 这意味着 a = b = c = 4m 我们可以将其半周长写为: S = a + b + c / 2 S = 4 + 4 + 4 /2 S = 12/2 = 6m 面积可以表示为: A = (6 (6 - 4) (6 - 4) (6 - 4))^1/2 A = (6 x 2 x 2 x 2)^1/2 A = 4 (3)^1/2 A = 6.93 m^2 因此,三角形的面积是 6.93 平方米。 亚历山大港的海伦海伦公式是以亚历山大港的海伦的名字命名的。他大约出生于公元 10 年,大约于公元 70 年去世。 他是罗马科学传统的代表。他的著作包括《Metrica》、《Mechanica》、《Automata》等。 让我们简要讨论他著名作品的描述。
海伦公式的三角学证明让我们讨论三种作为海伦公式证明的三角学方法。
余弦定理让我们讨论使用余弦定理的第一个证明。这意味着我们使用余弦定理公式来推导海伦公式。海伦在他的著作《Metrica》中提供了该公式的证明。 三角学证明与《几何公式》一书《Metrica》中讨论的证明截然不同。根据余弦定理:  其中, a、b 和 c 是三角形的边。 Alpha、beta 和 Gamma 是与三角形边相对的角。 下面一张图展示了具有三条边和三个角的三角形。   三角形的面积由以下公式给出: ½ x 底 x 高 其中,siny 是三角形的高。 因此,我们可以将三角形的面积表示为:  因此,海伦公式通过余弦定理得到了证明。 余切定理证明它也称为余切定理。它包括内切圆,如下图所示:  其中, a、b 和 c 是三角形的边。 Alpha、beta 和 Gamma 是与三角形边相对的角。  S 是半周长,由以下公式给出: S = (a + b + c)/2 面积可以计算为:  从上图可以看出,我们可以轻松计算角度的值。 Cot = 三角形的底边/垂线 Cot alpha = s - a/r 类似地,可以计算其他角度。 我们知道半角之和为 90 度。因此,我们也可以将面积计算为: A = rs  将两个不同的面积方程合并,我们得到:  这是所需的海伦公式。 勾股定理证明下图显示了一个直角三角形。  勾股定理适用于直角三角形,其中斜边的平方等于三角形另外两条边(底边和垂线)的平方和。 斜边被认为是三角形中最长的边。根据定理: (斜边)^2 = (底边)^2 + (垂线)^2 上图包含两个直角三角形。一个三角形由边 b、d 和 h 表示。另一个三角形由三条边 a、h 和 (c - d) 表示。 两个三角形的勾股方程可以写为:  使用勾股方程的三角形高度为: (垂线)^2 = (斜边)^2 - (底边)^2 将 d 和 h 的值代入勾股方程,我们得到: 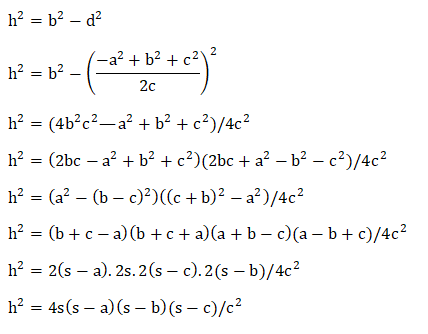 我们知道三角形的面积由以下公式给出: A = ½ x 底 x 高 A = ½ ch 因此,我们可以计算面积的值为:  这是海伦公式,已证明。 下一个主题综合科学选择题 |
?在理解Docker Swarm之前,我们需要了解“Docker”和“Swarm”这两个术语的含义。Docker Docker是一种工具,用于自动化应用程序作为轻量级容器的部署过程,以便特定应用程序可以在...
阅读 4 分钟
粉末是一种干燥、散装的固体,摇动或倾斜时可自由流动。它由许多极小的颗粒组成。虽然“粉末”和“颗粒”这两个标签有时被用来指代不同类型的材料,但粉末是颗粒的一个特定子集...
7 分钟阅读
简介 JSON(JavaScript 对象表示法)和 YAML(YAML 不是一种标记语言)是在定制文件类型方面有两种卓越的解决方案。由于其可读性、通用性和处理简单性,两者都经常用于存储配置文件。然而,每种格式都提供独特的组合...
7 分钟阅读
Drupal 是一个免费的开源内容管理系统(CMS),允许您组织、管理和发布您的内容。它建立在基于 PHP 的环境中。这是在 GNU,即通用公共许可证下进行的,这意味着每个人都可以下载并与他人分享。Drupal 是...
阅读 3 分钟
决策制定 决策制定是一个在行动过程中,为了达到目标而从一系列备选方案中进行选择的过程。决策制定的基本特征 它是一个人的过程,很大程度上需要运用思维。最终过程之前需要进行推理……
阅读 8 分钟
小组讨论 (GD) 是一种交流思想和观点的技术。它通常在专业或教育环境中实施。小组讨论的主要目标是为每个参与者提供表达他们对特定主题的想法和观点的机会,……
7 分钟阅读
什么是?cURL 代表客户端 URL。它是一个库,是 PHP 最强大的扩展。它允许用户在 PHP 中创建 HTTP 请求。cURL 库用于借助...
阅读 3 分钟
世界上的一切事物自然地处于持续运动状态。具体来说,地球似乎处于稳定状态;然而,它也或多或少地处于运动状态。这清楚地表明,地球上存在的一切事物也处于运动状态。尽管如此...
7 分钟阅读
养猫会非常有益。事实上,研究表明,仅仅观看猫的视频就能让你精力充沛。它们可能很可爱,甚至像依偎在你身边或发出咕噜声这样简单的行为也能带来快乐的好处。在……
阅读 4 分钟
引言 神圣的保护也许是天使数字777的意义所在。此外,一个天使可能正在试图与你沟通。有些人认为,当我们看到这些重要的数字时,我们的守护天使会试图引起我们的注意,并可能试图表达一个...
阅读 6 分钟
我们请求您订阅我们的新闻通讯以获取最新更新。

我们提供所有技术(如 Java 教程、Android、Java 框架)的教程和面试问题
G-13, 2nd Floor, Sec-3, Noida, UP, 201301, India
