Warshall 算法

Warshall 算法用于确定有向图的传递闭包或有向图的所有路径，通过使用邻接矩阵。为此，它会生成一个由 n 个矩阵组成的序列。其中，n 用于描述顶点的数量。

R(0), ..., R(k-1), R(k), ... , R(n)

在简单图中，顶点序列用于定义路径。在第 k 个矩阵（R^(k)）中，位于第 i 行和第 j 列的元素（r_ij^(k)）如果包含从 v_i 到 v_j 的路径，则其值为 1。对于所有中间顶点，w_q 是前 k 个顶点之一，这意味着 1 ≤ q ≤ k。

R⁽⁰⁾ 矩阵用于描述不含任何中间顶点的路径。因此，我们可以说它是一个邻接矩阵。R⁽ⁿ⁾ 矩阵将包含 1，如果它包含图中 n 个顶点中任何一个作为中间顶点的顶点之间的路径。因此，我们可以说它是传递闭包。

现在，我们假设一种情况，即 r_ij^(k) 为 1 且 r_ij^(k-1) 为 0。只有当存在从 v_i 到 v_j 且经过 v_k 的路径时，这种情况才成立。更具体地说，顶点列表的形式如下：

vi, wq (where 1 ≤ q < k), vk. wq (where 1 ≤ q < k), vj 

只有当 r_ik^(k-1) = r_kj^(k-1) = 1 时，上述情况才会发生。此处，k 为下标。

当且仅当 r_ij^(k-1) = 1 时，r_ij^(k) 才为 1。

因此，总而言之，我们可以说：

rij(k) = rij(k-1) or (rik(k-1) and rkj(k-1))

现在，我们将描述用于计算传递闭包的 Warshall 算法。

Warshall(A[1...n, 1...n]) // A is the adjacency matrix
R(0) ← A
for k ← 1 to n do
for i ← 1 to n do
for j ← to n do
R(k)[i, j] ← R(k-1)[i, j] or (R(k-1)[i, k] and R(k-1)[k, j])
return R(n)

此处，

• 该算法的时间效率为 O(n³)。
• 在该算法的空间效率方面，矩阵可以覆盖其前驱。
• 最坏情况成本为 Θ(n³)。我们应该知道，暴力算法优于 Warshall 算法。事实上，对于稀疏图，暴力算法也更快。

传递闭包示例

在本例中，我们将考虑两个图。第一个图描述如下：

该图的矩阵描述如下：

第二个图描述如下：

该图的矩阵描述如下：

这些图的主要思想描述如下：

• 顶点 i 和 j 将包含一条路径，如果：
• 图包含从 i 到 j 的边；或者
• 图包含一条经过顶点 1 从 i 到 j 的路径；或者
• 图包含一条经过顶点 1 和/或顶点 2 从 i 到 j 的路径；或者
• 图包含一条经过顶点 1、2 和/或顶点 3 从 i 到 j 的路径；或者
• 图包含一条经过任何其他顶点从 i 到 j 的路径。

在第 k 次迭代时，算法将使用编号为 1 到 k 的顶点（称为中间顶点），并找出 i 和 j 顶点之间是否存在路径。

在有向图中，具有 n 个顶点的**传递闭包**用于描述一个 n×n 的布尔矩阵 T。其中，第 i 行和第 j 列的元素为 1。这只有在从第 i 个顶点到第 j 个顶点存在有向路径时才会发生。否则，该元素为零。传递闭包描述如下：

**邻接矩阵**是一种方阵，用于表示有限图。在图中，矩阵的元素用于指示顶点对是否相邻。邻接矩阵也可以称为连接矩阵，它有行和列。一个简单的带标签图，其位置为 0 或 1，将由行和列表示。0 或 1 的位置根据顶点 V_i 和 V_j 是否相邻的条件分配。如果图包含两个节点之间的边，则分配为 1。如果图没有节点，则分配为 0。邻接矩阵描述如下：

**有向图**是由一对字符组成的。有向图描述如下：

Warshall 算法（矩阵生成）

将 R(k) 的元素与 R(k-1) 的元素联系起来的递推关系可以描述如下：

R(k)[i, j] = R(k-1)[i, j] 或 (R(k-1)[i, k] 且 R(k-1)[k, j])

为了从 R(k-1) 生成 R(k)，将执行以下规则：

**规则 1：** 在第 i 行和第 j 列，如果 R(k-1) 中的元素为 1，则在 R(k) 中它也将保持为 1。

**规则 2：** 在第 i 行和第 j 列，如果 R(k-1) 中的元素为 0，则 R(k) 中的元素将变为 1，前提是 R(k-1) 中第 k 行的元素和第 j 列的元素，以及第 i 行和第 k 列的元素都为 1。

Warshall 算法在有向图中的应用

为了理解这一点，我们将使用一个图，该图描述如下：

对于这个图，R(0) 将是这样的：

这里 R(0) 显示了邻接矩阵。在 R(0) 中，我们可以看到一条不含中间顶点的路径的存在。我们将借助 R(0) 中带框的行和列来获得 R(1)。

在 R(1) 中，我们可以看到一条包含中间顶点的路径的存在。顶点数不超过 1，这意味着只有一个顶点。它包含一条从 d 到 b 的新路径。我们将借助 R(1) 中带框的行和列来获得 R(2)。

在 R(2) 中，我们可以看到一条包含中间顶点的路径的存在。顶点数不超过 2，这意味着 a 和 b。它包含两条新路径。我们将借助 R(2) 中带框的行和列来获得 R(3)。

在 R(3) 中，我们可以看到一条包含中间顶点的路径的存在。顶点数不超过 3，这意味着 a、b 和 c。它不包含任何新路径。我们将借助 R(3) 中带框的行和列来获得 R(4)。

在 R(4) 中，我们可以看到一条包含中间顶点的路径的存在。顶点数不超过 4，这意味着 a、b、c 和 d。它包含五条新路径。

示例 1

在本例中，我们将假设 A = {1, 2, 3, 4}，并让 R 是 A 上的一个关系，其矩阵描述如下：

现在，我们将使用 Warshall 算法来计算 M_R∞。

解决方案

这里，矩阵是起点。所以矩阵描述如下：

现在，我们将假设 W₀ = M_R，然后依次计算 W₁、W₂、W₃ 和 W₄。（如果我们有一个包含 n×n 矩阵的 M_R，在这种情况下，我们将假设 W₀ = W_R 并计算 W₁、W₂、W₃、……、W_n。）对于每个 k > 0，Wk 是通过 W_k-1 的第 k 行和第 k 列计算得出的。因此，我们可以说 W₁ 是通过 W₀ = M_R 的第 1 列和第 1 行计算得出的，W₂ 是通过 W₁ 的第 2 列和第 2 行计算得出的，并且对于 W₃、W₄ 等也将遵循相同的过程。从 W_k-1 获取 W_k 的分步过程描述如下：

步骤 1

在此步骤中，我们将 W_k-1 中的所有 1 转移到 W_k 的相应位置。如果我们为此问题取 k = 1，则得到下表：

步骤 2

现在，我们将分别列出第 k 行中所有具有 1 的列，以及第 k 列中所有具有 1 的行。分离后，我们将得到列 1、2 和 4，以及行 1、2 和 3。

步骤 3

在此步骤中，我们将每一行号与每一列号配对。如果配对位置上没有 1，则我们将在 W₁ 的该位置添加 1。在所有空位置，我们将放入 0。

我们得到的配对描述如下：

(1, 1), (1, 2), (1, 4), (2, 1), (2, 2), (2, 4), (3, 1), (3, 2) 和 (3, 4)。

通过这些配对得到的矩阵描述如下：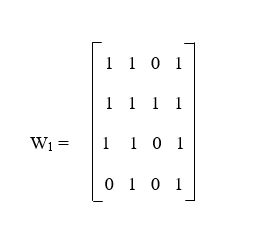

现在，我们将对 k = 2 重复相同的过程。第一步将为我们提供以下矩阵：

使用第二步，我们将得到行号 1、2、3、4 和列号 1、2、3、4。通过第三步，我们将得到 k = 2 的所有可能的行号和列号的配对，这些配对描述如下：

(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4), (4, 1), (4, 2), (4, 3) 和 (4, 4)。

通过这些配对得到的矩阵描述如下：

在此示例中，我们还将计算 W₃ 和 W₄，但我们知道 W₃ 和 W₄ 将得到与 W₂ 相同的结果。根据此算法，如果 W_k-1 中的一个条目是 1，则 W_k 的条目将保持为 1。因此，在 W_k+1、……、W_n 中也是如此。

因此：

传递闭包 R 可以定义为 A*A 的总关系，其中包含 A 的每个可能的有序对。因此，它可以指定 A 中的所有元素都通过

R^∞ 与 A 中的所有元素相关。

现在，我们将使用 {0, 1} 上的布尔运算 ∧ 和 ∨，以便更正式地理解此算法。如果 Wij(k) 是 W_k 的 (i, j) 条目，则根据上述步骤，我们可以说：

wij(k) = w(k?1)ij ∨ (w(k?1)ik ∧ w(k?1)kj) 

根据此算法的第二步，如果 i 存在于行列表中，j 存在于列列表中，则 w(k?1)ik∧w(k?1)kj=1 将为 1。如果此算法的第三步显示 w_ij^(k) 已经为 1（如第一步所示），或者 (i, j) 是第三步中形成的配对之一。