两个集合的对称差

在本文中，我们将讨论两个集合之间的对称差。在此，我们还将讨论两个集合之间对称差的性质。

希望本文能帮助您理解两个集合之间的对称差。

什么是对称差？

差集的另一种变体是对称差。假设有两个集合 A 和 B。两个集合 A 和 B 之间的对称差是包含同时存在于两个集合中但排除共同元素的集合。

两个集合之间的对称差也称为不相交并集。两个集合之间的对称差是那些同时存在于两个集合中但不存在于它们的交集中的元素的集合。两个集合 A 和 B 之间的对称差表示为A Δ B 或 A ? B。

我们可以通过示例来理解它。

示例 1 假设有两个集合包含一些元素。

集合 A = {1, 2, 3, 4, 5}

集合 B = {3, 5}

因此，给定集合 A 和 B 之间的对称差为 {1, 2, 4}

或者，我们可以说 A Δ B = {1, 2, 4}。

示例 2 假设有两个集合包含一些元素。

集合 A = {a, b, c, k, m, n}

集合 B = {c, n}

因此，给定集合 A 和 B 之间的对称差为 {a, b, k, m}

或者，我们可以说 A Δ B = {a, b, k, m}。

在下面的维恩图中，您可以看到两个集合之间的对称差。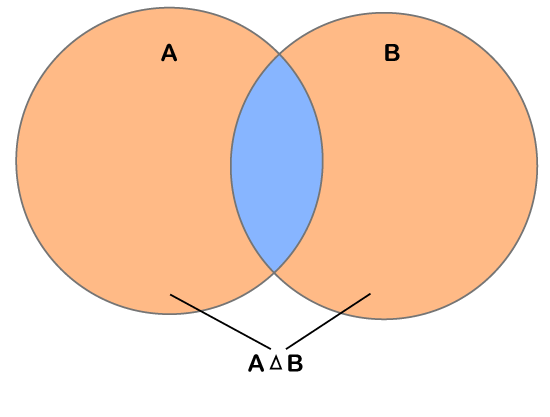

上面维恩图中用肤色着色的部分是给定集合之间的对称差，即 A Δ B。

让我们看一些属性来理解两个集合之间的对称差。

性质

两个集合之间的对称差的一些性质列出如下；

• 对称差可以表示为两个相对补集的并集，即，
  A Δ B = (A / B) ∪ (B / A)
• 两个集合之间的对称差也可以表示为两个集合的并集减去它们之间的交集——
  A Δ B = (A ∪ B) - (A ∩ B)
• 对称差既是可交换的，也是可结合的——
  A Δ B = B Δ A
  (A Δ B) Δ C = A Δ (B Δ C)
• 空集是中性元素（在数学中，中性元素是一种特殊的元素，当它与集合中的任何元素结合执行二元运算时，该元素保持不变。它也被称为同一元素）。
  A Δ ∅ = A
  A Δ A = ∅
• 如果集合 A 等于集合 B，则两个集合之间的对称差为——
  A Δ B = ∅ {当 A = B 时}

'两个集合的对称差' 与 '两个集合的差'

两个集合之间的差

两个集合 A 和 B 之间的差是指属于 A 但不属于 B 的所有元素的集合，并表示为 A - B。

示例：令 A = {1, 2, 3, 4}

和 B = {3, 4, 5, 6}

则 A - B = {3, 4} 且 B - A = {5, 6}

两个集合的对称差

两个集合 A 和 B 之间的对称差是包含 A 或 B 中但不同时存在于两者的所有元素的集合。它表示为 A Δ B 或 A ? B。

示例：令 A = {1, 2, 3, 4}

和 B = {3, 4, 5, 6}

那么 A Δ B = {1, 2, 5, 6}

现在，让我们看一些例子来更清楚地理解两个集合之间的对称差。

问题 1 - 假设您有集合 A = {10, 15, 17, 19, 20} 和 B = {15, 16, 18}。找出两个集合 A 和 B 之间的差，并找出它们之间的对称差。

解决方案 - 已知，

A = {10, 15, 17, 19, 20}

和 B = {15, 16, 18}

两个集合之间的差是——

A - B = {10, 15, 17, 19, 20} - {15, 16, 18}

= {10, 17, 19, 20}

两个集合之间的对称差是——

A Δ B = {10, 15, 17, 19, 20} - {15, 16, 18}

= {10, 16, 17, 18, 19, 20}

问题 2 - 假设您有集合 A = {2, 4, 6, 8} 和 B = {2, 5, 7, 8}。找出对称差 B Δ A。另外，绘制维恩图来表示两个给定集合之间的对称差。

解决方案 - 已知，A = {2, 4, 6, 8} 且 B = {2, 5, 7, 8}

我们知道 B Δ A = (B ∪ A) - (B ∩ A)

让我们尝试分步解决问题。因此，第一步是找出集合 A 和集合 B 的并集。

因此，(B ∪ A) = {2, 5, 7, 8} ∪ {2, 4, 6, 8}

= {2, 4, 5, 6, 7, 8}

之后，我们需要计算两个集合之间的交集。

(B ∩ A) = {2, 5, 7, 8} ∩ {2, 4, 6, 8}

= {2, 8}

现在，我们需要找出 A 和 B 集合的并集和交集之间的差，如公式所示，

所以，(B ∪ A) - (B ∩ A) = {2, 4, 5, 6, 7, 8} - {2, 8}

= {4, 5, 6, 7}

因此，B Δ A = {4, 5, 6, 7}

如上所述，“对称差是可交换的”，这将等于 A Δ B。现在，我们将通过维恩图来表示两个集合之间的对称差。

在维恩图中，首先，我们将绘制两个表示集合 A 和 B 的圆。如上计算，两个集合之间的交集为 {2, 8}，因此我们将这些元素列在相交区域中。然后，我们将剩余的元素列在各自的集合圆中，即集合 A 中的 {4, 6} 和集合 B 中的 {5, 7}。排列元素后，维恩图将是——

当我们查看上面的维恩图时，有一个全集 U。集合 A 和集合 B 都是全集 U 的子集。元素 {2, 8} 是相交的元素，因此它们在相交区域中表示。浅橙色区域是集合的并集，不包括相交区域。该区域是集合 A 和集合 B 之间的对称差，并将表示为——

B Δ A = (B ∪ A) - (B ∩ A) = {4, 5, 6, 7}

问题 3 - 假设您有集合 A = {5, 6, 8, 9, 10} 和 B = {2, 4, 7, 10, 19}。

证明对称差是可交换的，并使用给定的集合。

解决方案 - 已知，A = {5, 6, 8, 9, 10} 且 B = {2, 7, 8, 9, 10}

证明：A Δ B = B Δ A

取左侧 (LHS)，

A Δ B = (A ∪ B) - (A ∩ B)

(A ∪ B) = {5, 6, 8, 9, 10} ∪ (2, 7, 8, 9, 10}

= {2, 5, 6, 7, 8, 9, 10}

(A ∩ B) = {5, 6, 8, 9, 10} ∩ (2, 7, 8, 9, 10}

= {8, 9, 10}

所以，A Δ B = {2, 5, 6, 7}

现在，取右侧 (RHS)

B Δ A = (B ∪ A) - (B ∩ A)

(B ∪ A) = (2, 7, 8, 9, 10} ∪ {5, 6, 8, 9, 10}

= {2, 5, 6, 7, 8, 9, 10}

(B ∩ A) = (2, 7, 8, 9, 10} ∩ {5, 6, 8, 9, 10}

= {8, 9, 10}

所以，B Δ A = {2, 5, 6, 7}

因此，A Δ B = B Δ A

故，对称差是可交换的。